フロントドア基準(Front-door criterion)を知りたい方を対象に、導入編として書きました。
- Backdoor criterionに基づいた交絡因子の対処法は知っているけれど、この理論が使えない時に他の方法がないか知りたい。
- あと理論的な背景とかあれば、ついでに詳しく知りたい
という方を対象に記載しました。
なんとなく疫学手法の概念を理解できるよう、できるだけ平易な言葉で書きましたので、専門でない方でも興味があれば、読んでみてください。普段、統計学や疫学に関わる人が、どのように考えてデータ解析をしているか、少し親近感が湧くかもしれません。
本記事では下記の内容を解説します。
■ 本記事の内容
- Backdoor criterionのおさらい
- 計測できない交絡因子が残っている時の対処法
- Front-door criterionについて
今回はJudea Pearl(ジュディア・パール:UCLA)が記載したこちらの本を元に記載しています。詳しく知りたいからはp. 62からが該当ページですので、読んでみてください。疫学を生業にしている人は、こちらの本は必読書です。
■ Backdoor criterionのおさらい
まずはBackdoor criterionのおさらいをしましょう。
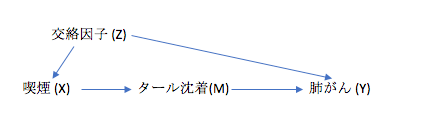
今回は喫煙(X)が肺ガン(Y)に与える影響を考えていきます。

「喫煙(X)が肺がんに与える影響」は「X→Y」の矢印に相当します。
一件すると、XとYのみの関係に注目すれば良さそうに見えますが、実はそう単純でもありません。よくみてみると、X←Z→Yのもう1つの経路があります。
XとYのみに注目して解析をした場合、
- 「X→Y」の経路(真の効果)
- 「X←Z→Y」の経路(偽りの相関)
を統計ソフトは見分けてくれません。
このため、偽りの相関の経路(「X←Z→Y」)を統計学的に対処する必要があります。
□ Backdoor criterionについて
なぜ「Backdoor」というのか、気になった方もいるでしょう。
矢印に注目すると、XからYへと向かっています。これは前向きですね。このため「X→Y」をFront-doorといいます。
一方で、ZからXへ入ってくる矢印「Z→X」はXからすれば後ろから入り込んできます。このため「X←Z→Y」をbackdoor path(裏道)と読んでいます。
*ちなみに、タール沈着(M)はX→Yの経路の途中にある媒介因子(Mediator)なので、基本的に統計学的な対処はしません。
Backdoor criterionでは、このbackdoor path(裏道)を閉じてあげれば、「X→Y」をみることができます。具体的な方法として、
- regression(回帰分析)
- g-computation (standardization)
- Inverse-probability weighting(逆確率重み付け)
などがあります。
DAGや数式で表すと、
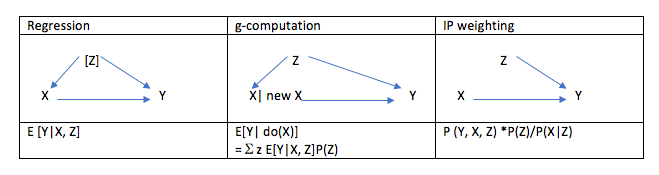
となります。
もう少し叙述的に言うと、
- 回帰分析(regression)では統計学的モデルにZを入れて対処する
- g-computationであれば、Zの分布を考慮して計測する
- IPWであれば、ZからXへ伸びる矢印を消し去る
という方法で統計学的にbackdoor path(裏道)を対処していると言えます。
Backdoor criterionの限界
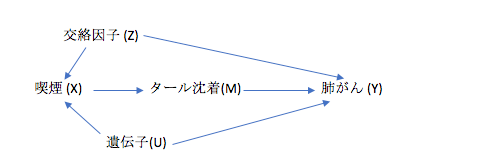
もうお察しの方も多いと思いますが、backdoor criterionの限界は、交絡因子(Z)が全て計測されている必要があります。
もし計測されていない交絡因子(U)を認めた場合、backdoor path(裏道:偽りの相関)は残ってしまいます。
この現象は、ほぼ全ての観察研究で起こっており、このため「観察研究では因果関係はいえない」とまで言われてしまうことがあります。(私はこの単純化は許容していませんが、説明はまたの機会に行います)
実例:Backdoor pathを閉ざせないケース

1950年代から喫煙が肺がんに与える影響は多数報告されていましたが、倫理的な側面や追跡期間の問題から観察研究でしか、この効果を計測できていません。
今もそうですが、1970年より前から、タバコ産業はタバコに反対する法案に抗おうと、様々な努力をしています。
そこで、このタバコ産業が提唱した理論は上のDAGになります。このDAGを説明すると、
- 遺伝子により喫煙の嗜好が決まる
- 遺伝子により肺がんが生じる
- 喫煙は肺がんの発症には直接は影響しない
という3つの情報が含まれています。
批判を恐れずに書くと、タバコ産業は「遺伝子という(当時)計測できない因子を持ち込んで、観察研究の結論を否定しようとした」とも言えます。
Backdoor pathは必ずしも閉じなくていい
「Backdoor pathを閉じないと(つまり、全ての交絡因子を対処しないと)、因果関係は証明できない」と発言する方もいますが、実はそうでもありません。
Backdoor pathを閉じなくても
- Instrumental variable method (操作変数法)
- Front-door criterion(フロントドア基準)
で因果効果をみることができるケースもあります。
計測できない因子があっても無力ではない

疫学者の得意とするg-method(上にあげた3つの手法など)の弱点は「計測できない因子(U)」の存在です。多くの観察研究で起こっている現象であるのは間違いないでしょう。
しかし、全く無力かというと、そうでもありません。
上のDAGをよくみてみましょう。
喫煙と肺がんの間に、肺へのタールの沈着という媒介因子(M)が存在します。この媒介因子(M)に注目して、計測されない交絡因子(U)があっても、因果関係を示唆できる方法を考案したのがJudea Pearl(ジュディア・パール)でした。
これが、Backdoor criterionに対して、Front-door criterionです。
簡単に説明すると、
- X →Mの矢印の効果を推定する
- M →Yの矢印の効果を推定する
- 1)と2)からX→Yの効果を推定する
という3段階で行います。
1. X→Mは推定可能である
XとMに交絡はありません。なぜなら、Uによる影響は、Yという合流点で閉ざされているからです。
このため、
E(M|do(X)) = E[M|X]
となります。これは簡単に推定できます。
2. M→Yも推定可能である
M→Yの経路は、「M←X←U→Y」での交絡があります。
しかし、この経路はXで閉じることができます。
これを数式にすると、
E[Y|do(M)] = Σx’ E[Y|M, X’]P(X’)
となります。
3. 1)と2)からX→Yの効果を推定する
最後に1)と2)で示した数式をつなぎ合わせてX→Yがわかります。
具体的には、
P(Y=y|do(X=x))
= Σm P(Y=y|do(M=m))P(m|do(X=x))
= ΣmΣx’ P(Y=y|M=m, X=x’)P(X=x’)P(M=m|X=x)
=ΣmΣx’ P(y|m, x’)P(x’)P(m|x)
= ΣmP(m|x) Σx’ P(y|m, x’)P(x’)
となります。
この数式は、フロントドアの公式(Front-door formula)として知られています。
Front-door criterion(フロントドア基準)に必要な前提
Front-door criterionに必要な前提として、
- M(媒介因子)はX→Yの経路を全てブロックできる
- XとMの間に交絡はない
- M→Yの経路は、Xで全てブロックできる
という3点になります。
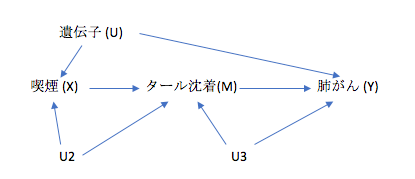
上のDAGのようにU2やU3があると、Front-door criterionを満たせなくなります。
まとめ
今回はfront-door criterionについて簡単に説明してきました。
もちろん観察研究ではbackdoorを閉じることは大事ですが、別にも手法があることは知っておいて良いと思います。
私自身はこの手法を実際の疫学研究で使用したことがまだないのですが、いつか試してみたいと考えています。
●疫学や統計学に携わる人は必読の書籍です。
交絡や交絡因子について