研究結果を解釈する際に、リスク(Risk)とオッズ(Odds)の違いは知っておいたほうがよいかもしれません。まず最初に、リスク(Risk)とオッズ(Odds)、リスク比(Risk ratio)とオッズ比(Odds ratio)について少し詳しく解説してみました。
リスクとは累積発生率(Cumulative Incidence)
疫学研究でいうリスク(Risk)は、累積発生率(Cumulative Incidence)のことを意味しており、一般の方々が考える「リスク(危険性)」とは異なる概念です。
累積発生率とは、「とある観察期間中にアウトカムを発症した人の割合」をいいます。
例えば、川崎病で入院した患者100人のうち、28日以内に冠動脈瘤(アウトカム)が発症した人が5人であった場合、累積発生率は0.05(5%)となります。
リスクを報告する際の注意点
累積発生率を報告する際の重要な点は、どのような母集団において(川崎病で入院した100人)、どの期間観察し(28日)、どのようなアウトカム(冠動脈瘤)が発症したのか、を明確にすることです。
疫学研究でリスク(Risk)を報告する場合は、基本的にはランダム化比較研究とコホート研究が中心になります。
リスクの利点と欠点
リスク(Risk)を報告する利点としては、直観的にわかりますし、差(Risk Difference)や比(Risk Ratio)を使用して2グループ以上で比較することができます(*Relative riskは、Risk differenceとRisk ratioを総称して使用します)。
注意すべき点としては、「28日以内の冠動脈瘤」のように、追跡期間を明確にする点です。また、追跡期間が長いと追跡不能(Loss to follow-up)の症例が増えてきて、選択バイアスを招いてしまう場合もあります。
また、リスク(Risk)は割合であるため、必ず0〜1の間になります。使用した統計モデルによっては(例、線形回帰分析linear regression)、0未満になったり、1以上になってしまうことがあるため、注意が必要です。
オッズはアウトカムが発生する確率と発生しない確率の比
一方で、オッズは、アウトカムが発生する確率(P)と発生しない確率(1-P)の比になります。このため、オッズはP/(1-P)となります。
オッズは何のために?
オッズは主にケース・コントロール研究や横断研究などで、オッズ比として使用し、Risk ratioなどを推定するために利用されることが多いです。
例えば、稀なアウトカムを発生した症例をケースとして抽出し、アウトカムは発生しなかったが稀なアウトカムを発生し得た母集団からコントロールをランダムにサンプルする方法を、cumulative samplingと言います。
詳しい数式的な証明は省略しますが、このcumulative sampling法を使用した場合、odds ratioはrisk ratioの近似値となります。
つまり、ケース・コントロール研究をすることで、コホート研究をせずとも、risk ratioを推定することが可能になるのです。
これはケース・コントロール研究を行うメリットの1つと考えられています。
なぜなら、稀なアウトカムをコホート研究で行おうとすると、かなりの症例数の追跡が必要となり、莫大なコストを要するためです。ケース・コントロール研究では、効率的に稀なアウトカムを集め、コントロールをサンプルするため、研究に必要な時間とコストを大幅に減らすことができます。
オッズの数学的な利点
また、オッズはリスクとはことなり、0〜無限大の値をとることができます。ロジスティック回帰分析では、log odds(ログオッズ)を使用することで、マイナス無限大〜プラス無限大の値をとることができるという、数学的なメリットもあります。
リスクのように0〜1の外に出てしまう心配をしなくてよいのです。
アウトカムが稀であれば、リスクとオッズは近似する
とある疾患が起こるリスクをPとすると、オッズはP/(1–P)でした。このリスクが非常に稀である場合、「(1–P)≒1」となるため、リスクとオッズは近似します。逆に、アウトカムが稀でない場合、リスクとオッズは乖離してしまいます。以下の図をみてください。
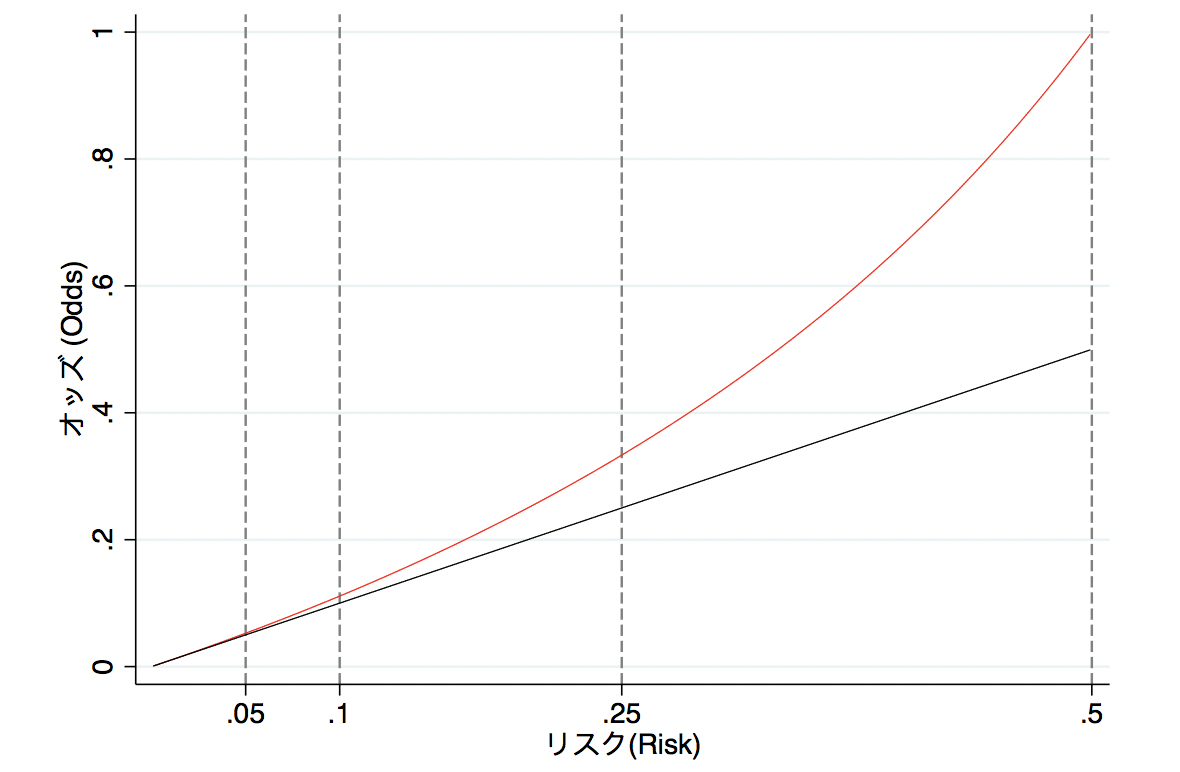
赤色線は「オッズvs. リスク」をプロットしたもので、黒色線は「リスクvs. リスク」でプロットしたものです。リスクが低い場合(< 0.05)、オッズとリスクの乖離が少ないのが分かります。一方で、リスクが高くなるにつれ、オッズとリスクの乖離が大きくなります。このように、リスクとオッズが近似するのは、リスクが低い場合、つまりアウトカムとするイベントが稀の場合のみです。
リスク比とオッズ比について
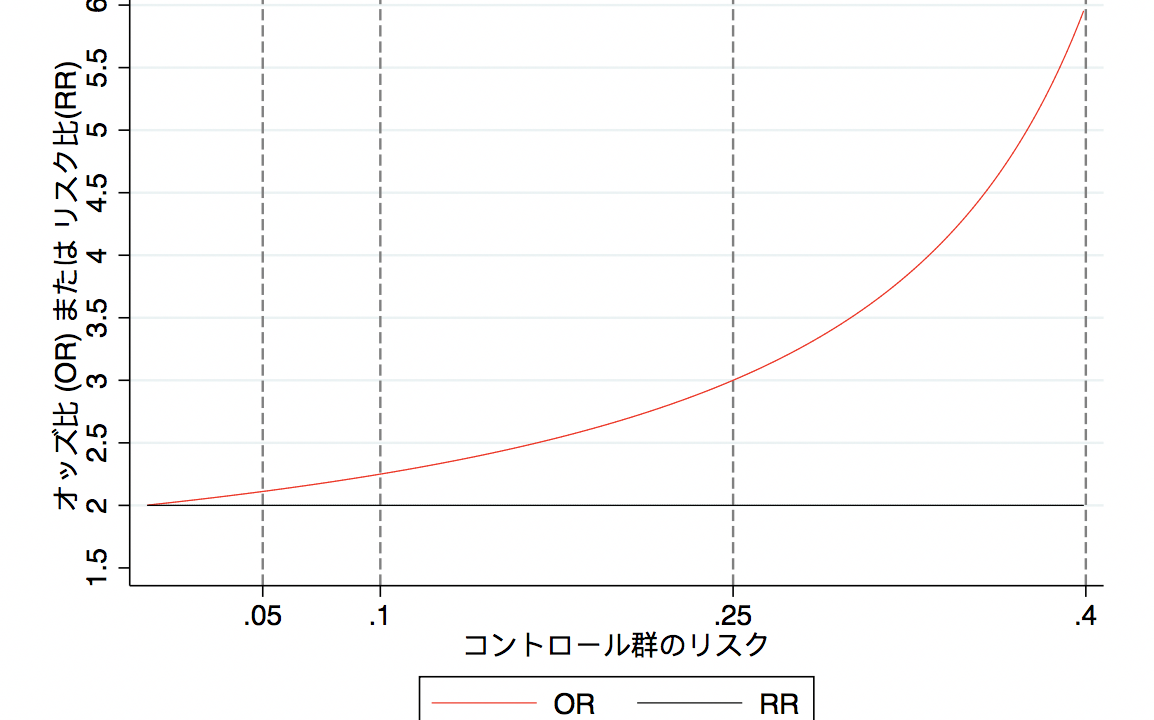
さらに、リスク比(Risk Ratio(RR))とオッズ比(Odds ratio(OR))でも考えて見ましょう。今回は、リスク比 (RR) を2に固定して、コントロール群のアウトカムが生じるリスクによって、オッズ比とリスク比がどのように乖離するのかをみていきましょう。
例えば、コントロール群のリスクが0.1だった場合、治療群のリスクは0.2となり、リスク比は2.0です。一方、オッズ比は(0.2/0.8)/(0.1/0.9) = 2.25となります。リスク比2.0 vs. オッズ比2.25と少し乖離があるのが分かります。同様に、コントロール群のリスクを0.01, 0.2, 0.25…などと動かしてシミュレーションをしてみると、以下のようになります。
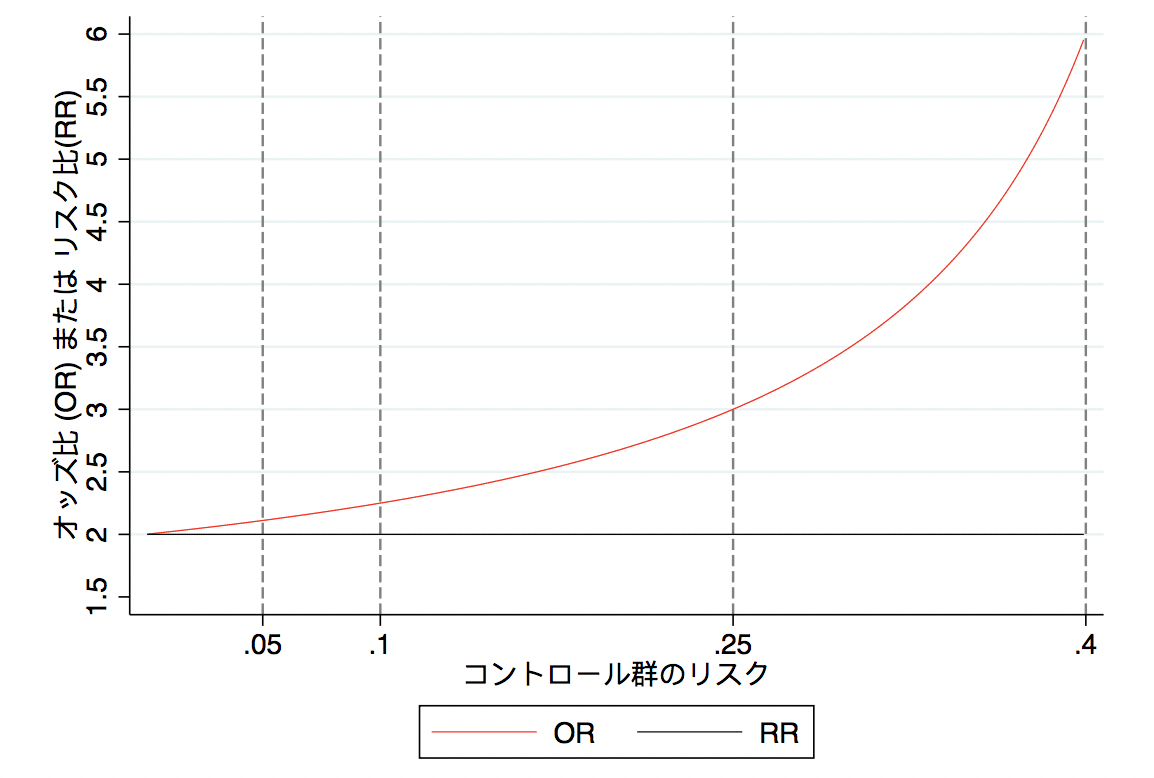
常にRR = 2.0で固定していましたが、コントロール群のリスクが高くなるにつれ、ORはRRから乖離しているのがわかるとおもいます。例えば、コントロール群のリスクが0.4で、RRが2であった場合、これをORにすると6になります。同じ結果でも、RRで2倍というのと、ORで6倍というのが、随分と印象がかわってしまうのではないでしょうか。
溶連菌感染症における第3世代セフェム5日間vs.ペニシリン10日間
さて、これまでの解説を、研究結果に当てはめて見ましょう。
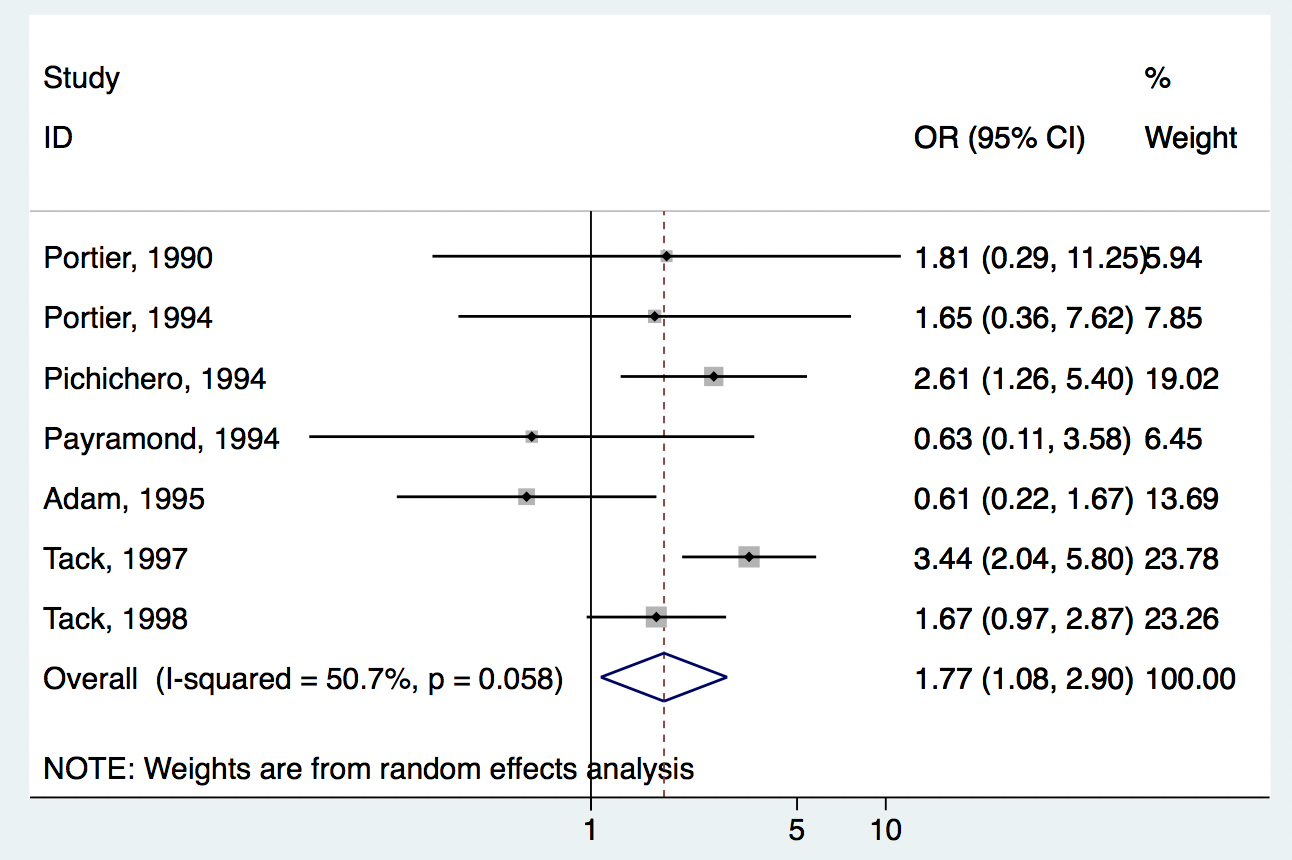
こちらの結果は、第3世代セフェム5日間とペニシリン10日間の治療を比較したRCTのメタ解析の結果でした。(Casey JR, Pichichero ME. Metaanalysis of short course antibiotic treatment for group A streptococcal tonsillopharyngitis. Pediatr Infect Dis J. 2005;24(10):909-917. doi:10.1097/01.inf.0000180573.21718.36)
ペニシリン10日間と比較して、第3世代セフェム5日間投与したグループは、除菌成功するオッズが1.77倍(95%CI, 1.08〜2.90)でした。
「オッズが1.77倍」といわれると、第3世代セフェム5日間投与のほうが、随分と有効そうな印象を受けてしまいます。
ORをRRに変換すると…
ここで、全く同じ結果を、RRに変換してみましょう(*上のメタ解析の結果と同じく、ランダム効果モデルにinverse variance weightを使用しています)
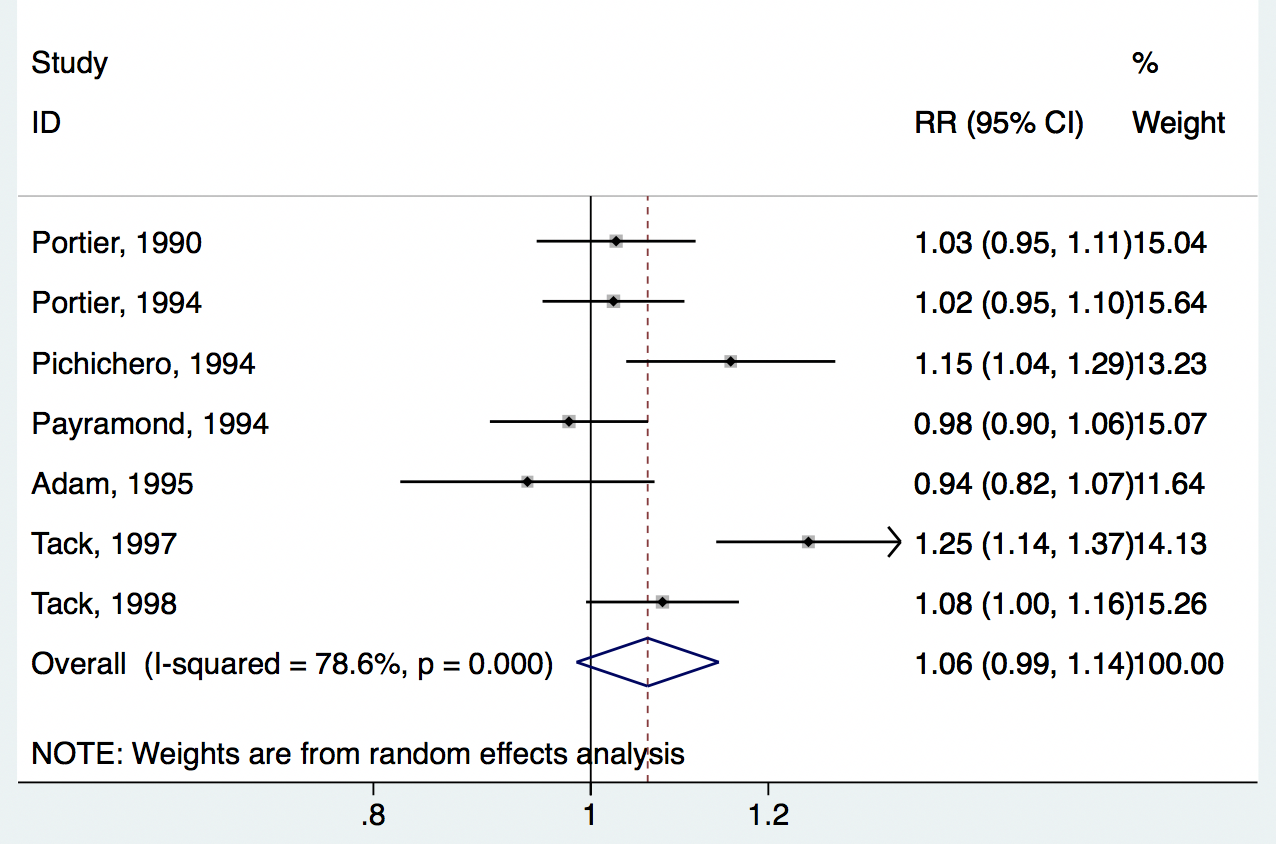
ペニシリン10日間と比較して、第3世代セフェム5日間投与したグループは、除菌成功するリスクが1.06倍(95%CI, 0.99〜1.14)でした。オッズ比は1.77倍でしたが、リスク比は1.06倍です。
随分と異なる印象をうけるのではないでしょうか?
おわりに
オッズとリスクは異なる概念です。
アウトカムが稀であれば、オッズとリスク、オッズ比とリスク比を近似して解釈できるのですが、稀でない場合は、オッズやオッズ比は過大評価してしまうケースがあります。
今回の第3世代セフェムとペニシリンの比較のように、メタ解析の結果ですら注意して読み解きたいところです。
疫学の教科書はこちらがおすすめ
メタ解析の教科書はこちら
(2025/04/19 10:13:08時点 Amazon調べ-詳細)