- 『Hibワクチンって効くのでしょうか?』
- 『小さな子供にワクチンを打って大丈夫でしょうか?』
- 『ワクチンをするなら、有効性が確かなものがいいと考えています』
など、ワクチンに関する質問は様々です。また、質問はしなくても、ワクチンの有効性をきちんと理解できている方は少ないでしょうし、ワクチンを推奨する小児科医ですら、どの程度の有効性が確実に理解できている方は多くはないかもしれません。
今回はヒブ(Hib)ワクチンの投与回数と有効性を示したメタ解析の論文をピックアップしました。原文はこちらになります。
ヒブ(Hib)感染症そのものについてはこちらで詳しく解説しています。
Hibとはインフルエンザ桿菌の略語で、感染すると
- 髄膜炎
- 菌血症
- 肺炎
- 喉頭蓋炎
- 骨髄炎・ 関節炎
などを起こします。特に3−4歳未満の乳幼児は感染しやすいため、ワクチンで予防が行われています。
今回のこちらの論文では、Hibワクチンの投与回数と有効性を検討しています。
研究の方法
今回の研究では、
- ランダム化比較研究、準ランダム化比較研究
- 5歳未満の小児
を対象にヒブワクチンの投与回数と有効性を検討しています。
ワクチン投与群と非投与群で、侵襲性ヒブ感染症のリスクを比較しています。
統計解析について
統計解析では固定効果モデル(Fixed-effect model)を使用してワクチンの効果を検討しています。
- Risk Ratio (RR)を計算し、
- ワクチン効果(VE)= (1 – RR)x 100%
と計算しています。
研究間のばらつきの評価はQ testが行われています。
研究結果と考察
9つの研究がメタ解析に組み込まれました。
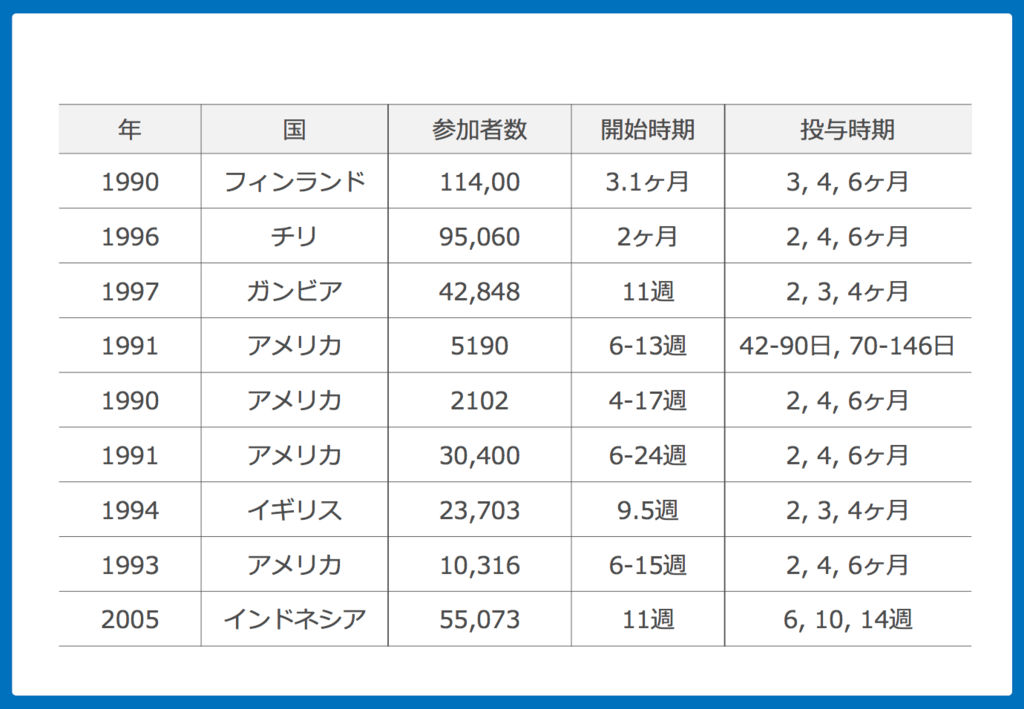
研究間でのばらつきは統計学的には認めませんでした。
ワクチンの有効性
ワクチンの有効性は
- 3回投与:82% (RR 0.18; 95%CI 0.13-0.27)
- 2回投与:79% (RR 0.21; 95%CI 0.10-0.47)
- 1回投与:65% (RR 0.35; 95%CI 0.16-0.47)
となっています。
1歳未満は投与回数が多いほうがヒブによる重症感染症を予防できているといえます。
きちんとスケジュール通りワクチンをすることの重要性がわかります。
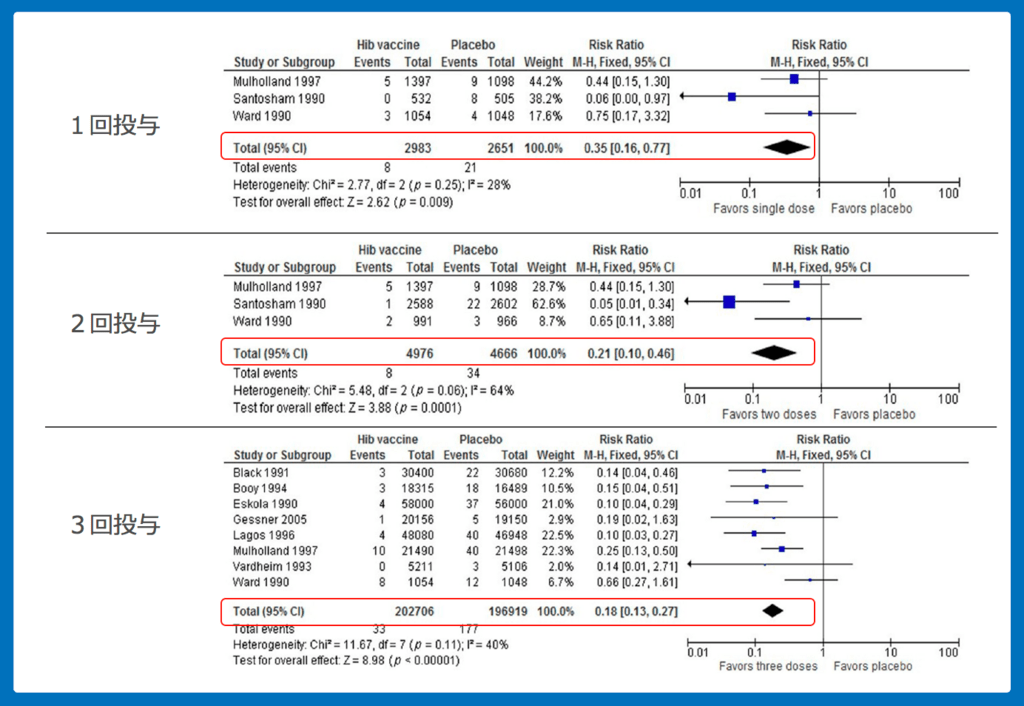
*1回投与、2回投与の例はスケジュールがイレギュラーなのもあり、研究数が少ないですね。
出版バイアスについて
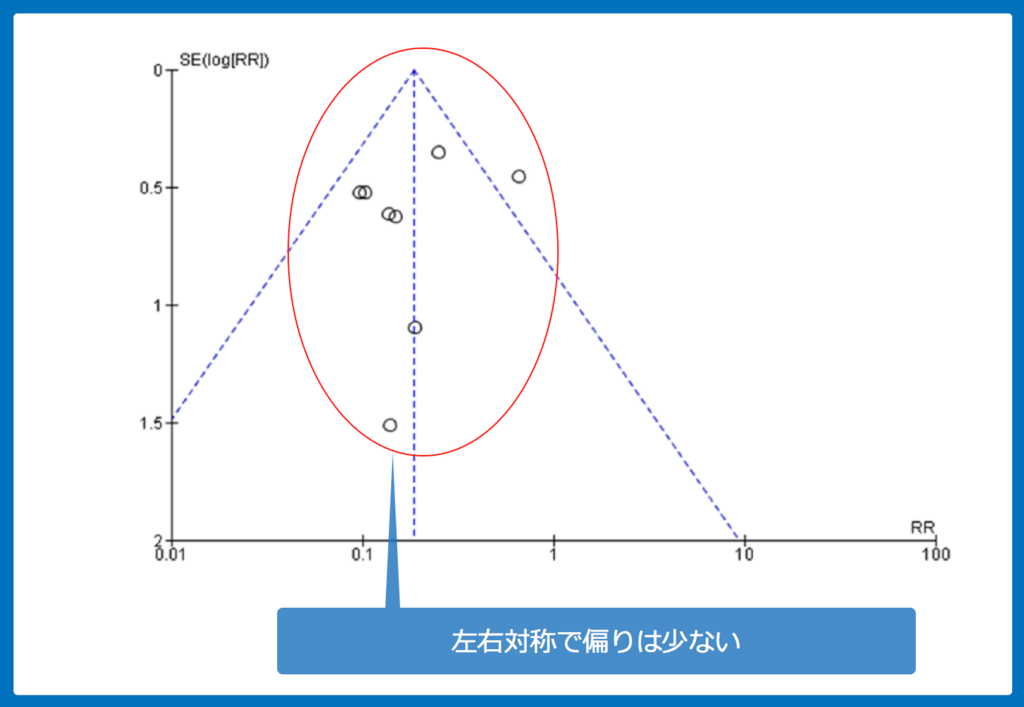
Funnel Plotという手法で出版バイアス(Publication bias)を評価していますが、比較的左右対称になっており、バイアスは少ないと判断されています。
Meta-regression
今回の論文ではワクチンの接種回数が0回、1回、2回、3回と分かれているのですから、この関係性をみてもよいと思いました。
メタ解析でもこれは可能で「Meta-regression」といわれます。
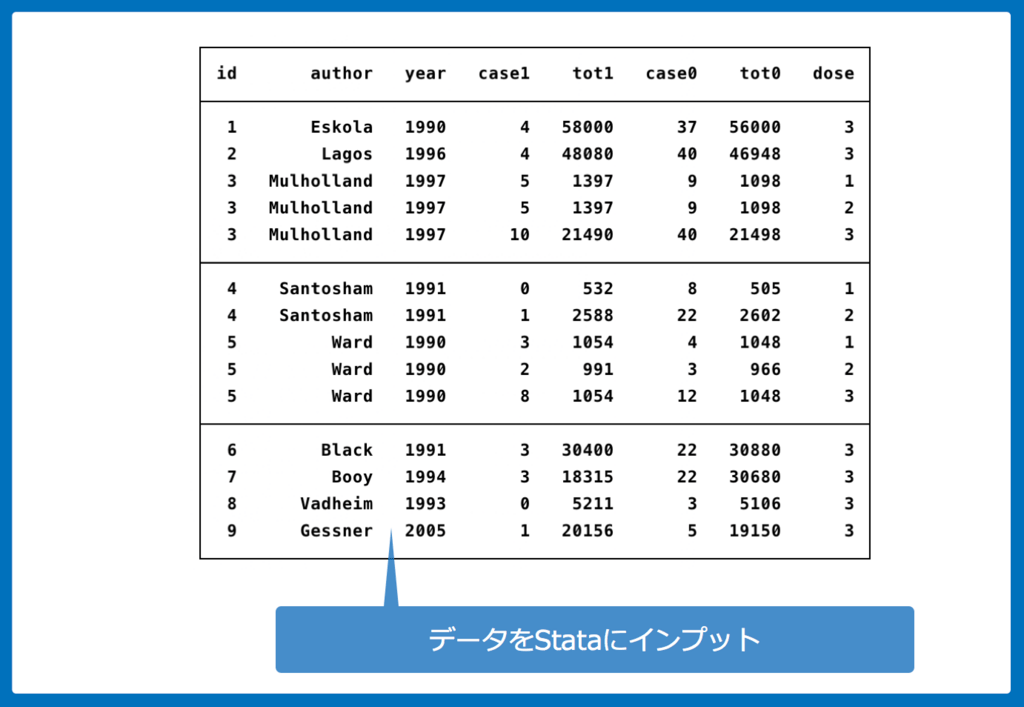
データのインプット
論文上にきっちりとデータが記載されているため、これを利用してStataにインプットします。
グラフでそれぞれの投与回数のRRを比較
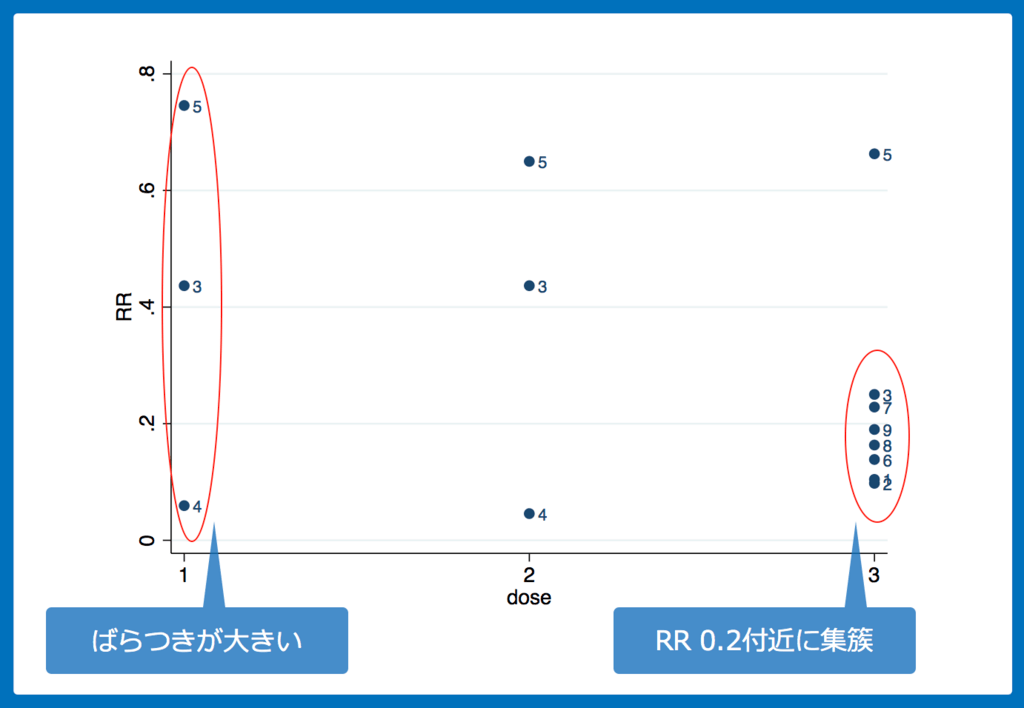
投与回数1回と2回のデータは少ないですが、ワクチンの有効性はRRで0.1〜0.7くらいとかなりばらつきが大きいです。
一方で、3回投与している場合は、RR 0.2付近に集簇しています。
これをMeta-regressionしてみましょう。
Meta-regression
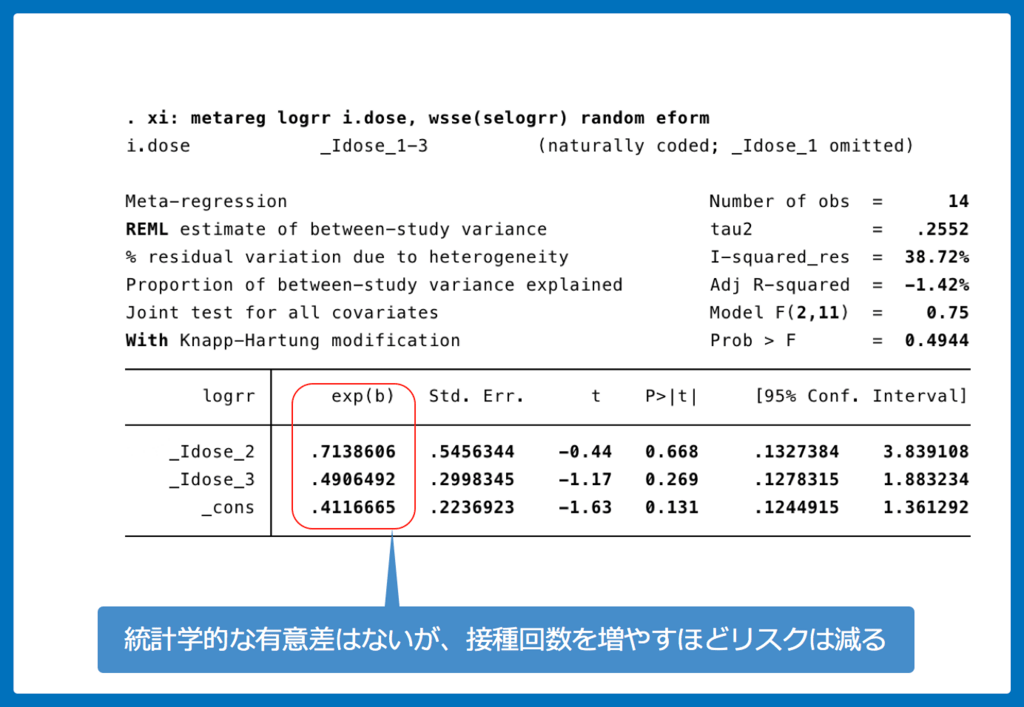
そもそも1歳未満で1回接種、2回接種した研究数は少ないため、統計学的な有意差は出ませんでしたが、接種回数を2回するとリスクは0.7倍、3回にすると0.4倍に低下します。
(解析コードは最後にあります)
Dose-response meta-analysisという手法もあります。またの機会にご紹介できればと思います。
まとめ
ヒブワクチンはインフルエンザ桿菌による重症感染症のリスクを80%ほど減少させます。
1歳未満で3回接種ですが、3回確実に接種したほうがよいでしょう。
あわせて読みたい
使用した解析コードはこちら
| clear | |
| input id str16 author year case1 tot1 case0 tot0 dose | |
| 1 "Eskola" 1990 4 58000 37 56000 3 | |
| 2 "Lagos" 1996 4 48080 40 46948 3 | |
| 3 "Mulholland" 1997 5 1397 9 1098 1 | |
| 3 "Mulholland" 1997 5 1397 9 1098 2 | |
| 3 "Mulholland" 1997 10 21490 40 21498 3 | |
| 4 "Santosham" 1991 0 532 8 505 1 | |
| 4 "Santosham" 1991 1 2588 22 2602 2 | |
| 4 "Santosham" 1991 | |
| 5 "Ward" 1990 3 1054 4 1048 1 | |
| 5 "Ward" 1990 2 991 3 966 2 | |
| 5 "Ward" 1990 8 1054 12 1048 3 | |
| 6 "Black" 1991 3 30400 22 30880 3 | |
| 7 "Booy" 1994 3 18315 22 30680 3 | |
| 8 "Vadheim" 1993 0 5211 3 5106 3 | |
| 9 "Gessner" 2005 1 20156 5 19150 3 | |
| end | |
| list | |
| *Calculate RR and log(RR) | |
| gen non1=tot1-case1 | |
| gen non0=tot0-case0 | |
| replace case1 = 0.5 if case1 == 0 | |
| replace case0 = 0.5 if case0 == 0 | |
| gen rr = (case1/tot1)/(case0/tot0) | |
| gen logrr=log((case1/tot1)/(case0/tot0)) | |
| gen selogrr=sqrt((non1/(case1*tot1)) + (non0/(case0*tot0))) | |
| list id selogrr | |
| graph twoway (scatter rr dose, mlabel(id)), /// | |
| graphregion( color(white) ) plotregion( fcolor(white) ) /// | |
| legend(off) xtitle(dose) ytitle(RR) /// | |
| xlabel(1(1)3) | |
| *meta-regression | |
| xi: metareg logrr i.dose, wsse(selogrr) random eform |

 by
by