前回、システマティック(系統的)レビューとメタ解析における異質性(Heterogeneity)と均質性(Homogeneity)について説明してきました。
これらの評価は統計学的に行われ、
- Cochran Q Test
- I-squared
- L’Abbé plot
が代表的です。今回はこの3つを簡単に解説していこうと思います。
Cochran Q Testについて
Cochran Q Testは仮説検定ですので、
- 帰無仮説(H0)と対立仮説(HA)を設定
- Q値を計算
- P値を算出する
という3つの作業を行います。
1. 帰無仮説(H0)と対立仮説(HA)
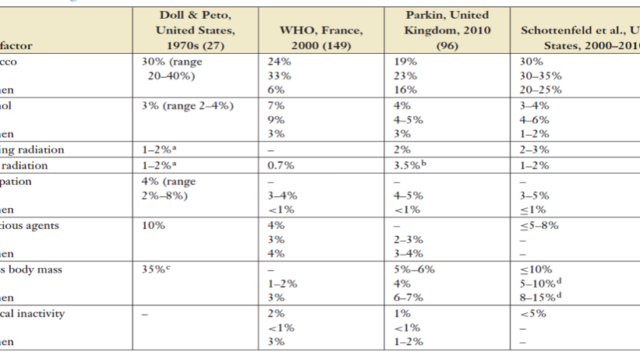
治療効果を計測するには沢山の指標があります(Odds Ratio, Rate Ratio, Risk Ratio, Risk Differenceなど)。
この計測された治療効果のことを「Effect Estimate(θ)」といいますが、今回はRisk Ratio(RR)を例に考えていきましょう。
まず、帰無仮説(H0)と対立仮説(HA)を叙述的に表現してみると
- H0: 治療効果は全ての研究で一定である
- HA: 治療効果は全ての研究で一定ではない
となります。メタ解析に入れた研究が10個あったとすると
- H0: RR1 = RR2 = RR3 = … = RR10
- HA: 少なくとも1つのRRは他のRRと異なる
(At least one of RRs is different from the others)
とRRと数式を使って表現できます。
2. Q値を計算する
次にQ値を計算します。Q値は
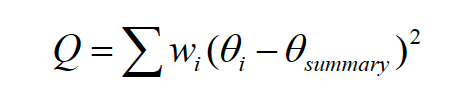
で計算できます。θi は個々それぞれの治療効果(今回はそれぞれの研究のRR)、θ summaryはメタ解析から得られた全体の治療効果(Pooled RR)となります。
「Wi」は個々の研究の重み付けで、分散の逆数(Inverse Variance)を使用します。
*Q値を計算するには、一度、メタ解析をして Pooled Estimateを計測する必要があります。
例えば、以前、私のブログで紹介したBCGの有効性をみたメタ解析を例に考えてみましょう。
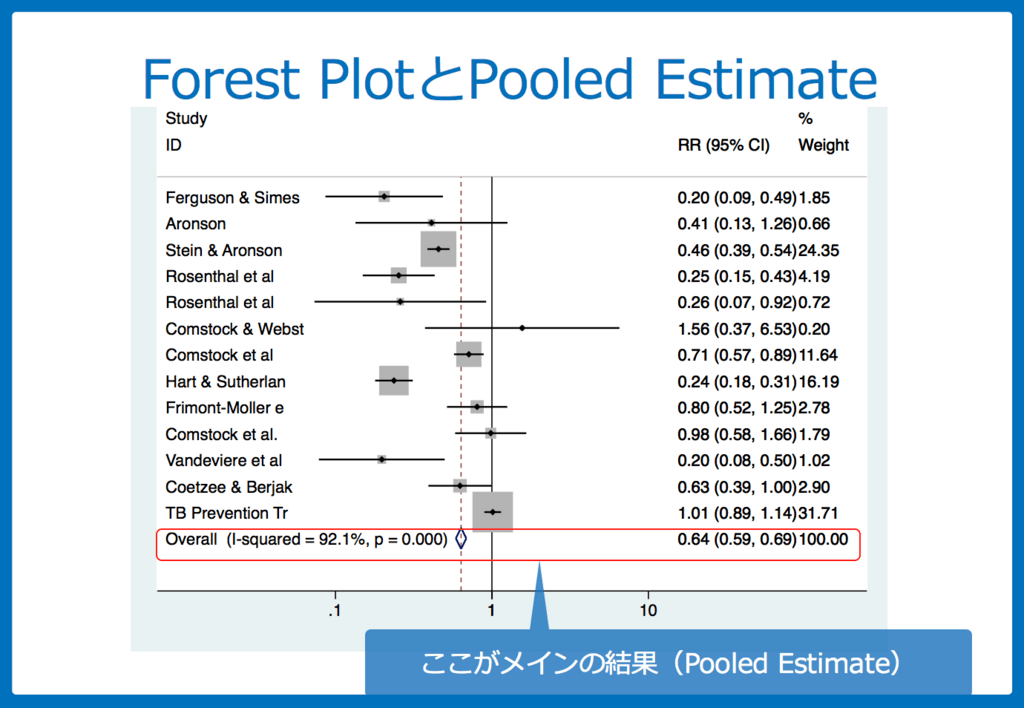
こちらが研究結果でした。
- 個々のRisk Ratio(RR)とSummary RR (= 0.64; pooled estimate)の差を二乗し
- weightをさらにかけ
- それぞれを足す
という作業をすればQ値が計算できます。
普通は面倒なので統計ソフトにこれを指示すると以下のようにアウトプットがでます。
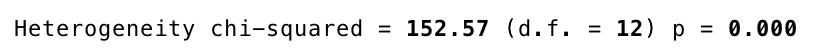
このHeterogeneity Chi-squaredがQ値になります。
3. P値を計算する
今回の研究は13個ありますので、自由度(df)= 13 – 1 = 12です。
Q値はカイ二乗分布を仮定しており、P値 < 0.001のため帰無仮説は棄却されます。
よって「少なくとも1つのRRは、他のRRと異なる」=「異質性(Heterogeneity)がある」と統計学的に判断します。
統計学的な評価の注意点
この異質性(Heterogeneity)の評価は、研究数やそれぞれの研究のサンプル数に依存します。
異質性の検定をしても統計学的に有意差がでづらい傾向にあり、「偽陰性(本当は異質性があるが、ないと評価する)」となることがあります。
帰無仮説が棄却できなくても、本当に帰無仮説が正しいかわかりませんので、解釈に注意しましょう。
I-squared (I二乗)について
I-squaredは、Q値が分かれば以下の公式で簡単に計算できます
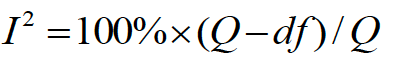
今回の場合;
- Q = 152.57
- df (自由度) = 12
のため、I-squared = 100% x (152.57 – 12) / 152.57 = 92.1%となります。
95%信頼区間の計算も可能で、統計ソフトを用いると88%〜95%という結果になりました。

I -squared と異質性(Heterogeneity)
Cochran-QとP値のように、厳格なカットオフはないのですが;
- <25%:異質性は低い(Low Heterogeneity)
- 25〜75%:異質性は中等度(Moderate Heterogeneity)
- >75%:異質性は高度(Large Heterogeneity)
となっています。今回の例は92.1%であったため、異質性が高いといえます。
I-squaredの真の意味
I-squaredは以下のように数式で表現することもできます;
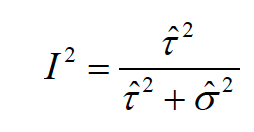
ここで「τ(タウ)」と「σ(シグマ)」の意味ですが
- τ(タウ)= 研究間のばらつき
- σ(シグマ)= 研究内のばらつき
を意味します。I-squaredの値が大きい(100%に近い)のは、それぞれの研究間でのばらつきが大きいことを意味します。
もうすこし砕いて説明すると、それぞれの研究結果のばらつきが大きい、つまり均質でない(= 異質である(Heterogeneity))という意味になります。
L’Abbé Plotについて
今回の研究をこの手法で図示すると
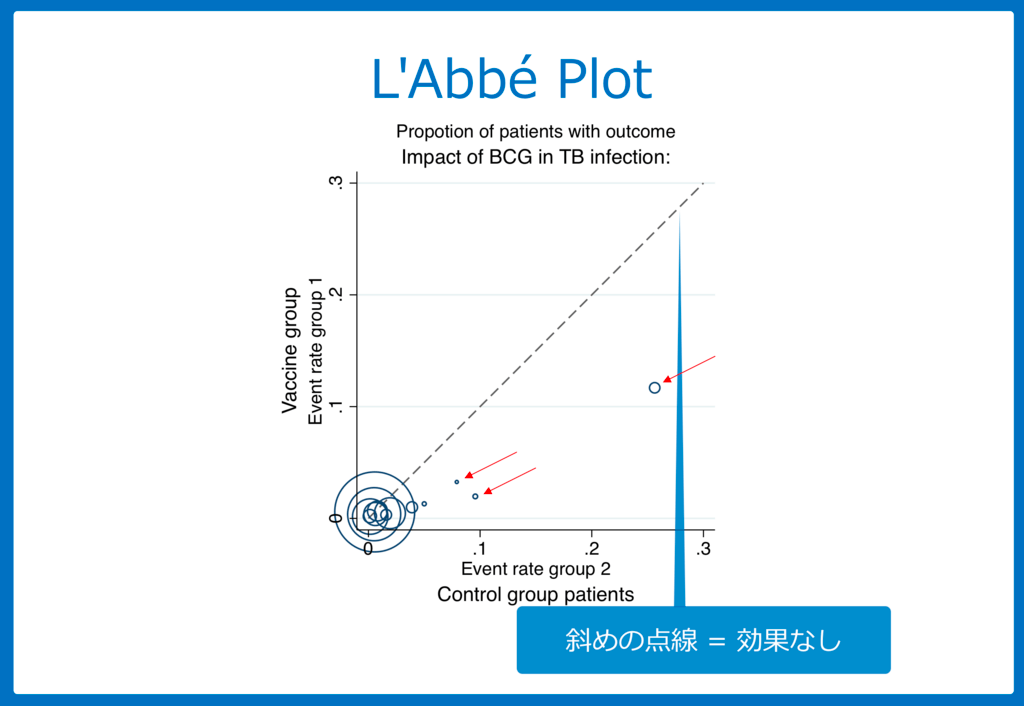
この図の読み方ですが、
- Y軸:ワクチン接種群のアウトカム発症率
- X軸:ワクチン非接種群のアウトカム発症率
- 斜めの点線:効果なしのライン
となっています。
赤矢印で示した研究は、その他の研究から外れているのがわかると思います。
つまり、これらの研究が異質性の元になっていると図から判断できます。
異質性(Heterogeneity)を認めたらどうすればよいか?
Heterogeneity(異質性)を認めた場合、そのままメタ解析をしてPooled Estimateを計算することはできません。
なぜなら、メタ解析の手法は、そもそも「Heterogeneity(異質性)はない」という仮定のもと行われているからです。
この場合、Heterogeneity(異質性)の原因となっている別の因子(効果の修飾因子:Effect Modifier)を探し出す必要があります。
もし該当する因子があれば
- サブグループ解析をする
- メタ回帰分析(Meta-regression)をする
の2通りの方法があります。メタ回帰分析については、またの機会に詳しくお話します。
まとめ
今回は Heterogeneity(異質性)の統計学的な評価の仕方を説明してきました。
次回は固定効果(Fixed Effect)とランダム効果(Random effect)について解説していこうと思います。