先日、感染症科の先生方に「感染症疫学(Infectious disease epidemiology)」について色々と質問される機会がありました。
感染症疫学の手法は、普段の研究で使う機会が乏しいのもあって、気がつくと色々と忘れて、また本を読み直してを繰り返しているため、今回は備忘録としてこちらに分かりやすく記載させていただきます。
Lowell Reed(1937)について
上の写真の人物は誰か、気になっているでしょう。
感染症疫学を生業にしている人なら、Lowell Reedを知らない人はいないでしょう(もし知らなければ、その方はもぐりだと思ってください)。
彼は感染症疫学のなかで非常に有名なS-I-Rモデル(別名:Reed-Frost epidemic model)を考案した研究者です。
S-I-Rは
- Susceptible(免疫のない人たち)
- Infected(感染した人たち)
- Recovered and Immune(感染が軽快して、免疫を獲得した人)
の頭文字をとったものです。
S-I-R の例
例えば身近なインフルエンザに免疫のない人たち(S)の一部が感染して(I)、最後に回復して免疫を得る(R)、という順に起こります。
この(数理)モデルのことを、S-I-Rモデルといいます。
R0 と R について
S-I-Rモデルの解説の前に、感染症疫学の基本となる
- R0:基本再生産数(Basic Reproductive Number)
- R:実効再生産数(Effective Reproductive Number)
の2つがありますが、今回はR0について解説します。
R0(基本再生産数:Basic Reproductive Number)について
基本再生産数(R0)はその名の通り、「基本(最初)」に感染症が「再生産」される理論上の「数」のことをいいます。
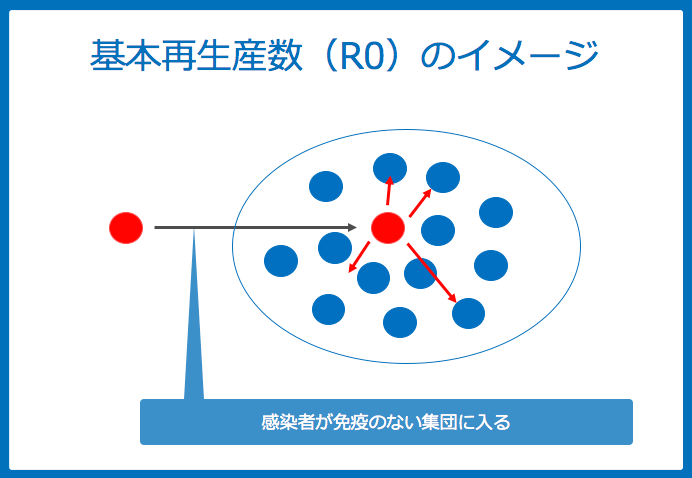
もうすこし分かりやすく説明すると、新規に感染症にかかった1人が、(免疫をもたない)集団に入った場合、感染させることができる人数のことをいいます。
これは流行の初期と考えるとイメージしやすいかもしれません。
R0が1より大きいと流行する可能性がある
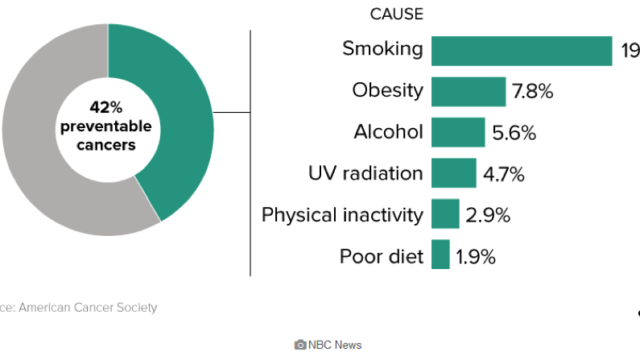
基本再生産数(R0)は1より大きいか否かが重要で
- R0 > 1:感染症が流行する
- R0 < 1:感染症は流行せず終息する
と考えられています。
R0 に影響する因子について
基本再生産数(R0)は理論上の数値ですが常に一定ではなく、様々なことから影響を受けます。
例えば、
- ウイルスなど病原体の性質
- 集団がとる行動
- 社会的な環境
によって値が変動します。
例えば、麻疹は空気感染をする性質のある病原体ですので、感染する範囲が広がりやすく、R0は高くなります。
同じ麻疹でも、人口の密集した都市部で起こるのと、人口の少ない過疎地で起こるのでは R0 が異なります。都市部のほうが人と人との接触が多いので、R0 が高くなるのは当然でしょう。
R0 は3つの指標で数式化
基本再生産数(R0)を3つの指標でシンプルにすると、以下のようになります
- R0 = (感染力) x (接触回数) x (感染力のある期間)
感染力は、1回の接触で感染する割合といえます。
これに接触回数と感染力のある期間を掛け合わせたものが R0 になります。
R0の具体例
では、実際にR0がどのくらいか、みてみましょう。代表的な感染症ですと、
- 麻疹:12〜20
- 風疹:6〜7
- おたふく:4〜7
- ジフテリア:6〜7
- 結核:5
- 天然痘:5〜7
- ポリオ:5〜7
- HIV:2〜5
- エボラ:1.5〜2.5
と報告されています。
R0は医療政策で重要
基本再生産数(R0)は以下でした:
- R0 = (感染力) x (接触回数) x (感染力のある期間)
R0は医療政策で非常に重要です。
なぜなら、理論上、R0 < 1にしてしまえば、感染症の流行が阻止できるためです。
1. 接触回数を減らせばR0は下がる
R0の要因として、接触回数がありました。
例えば、新規に重症な感染症が発症した場合、発症した患者と接触者は隔離される可能性があります。
これは、隔離は「接触回数」を減らすためR0が低下するため、流行を防ぐことができるためです。
(*倫理的な側面は今回は考慮していないので、この点はご容赦ください)
2. 感染力のある期間を短くできればR0は下がる
あるいは、治療で感染力のある期間を短くできれば、R0は低下して流行を防ぐことができるかもしれません。
例えば結核のR0は6でした。
このR0 = 6は無治療の母集団で計算され、さらに無治療の場合、感染力は52週間あると仮定します。(*極端な例ですが、ご容赦ください)
治療により感染力のある期間が52週から6週に短くできた場合、R0は
- R0 = 5 x (6/52) = 0.6 < 1
となります。
ワクチン接種率とR0について
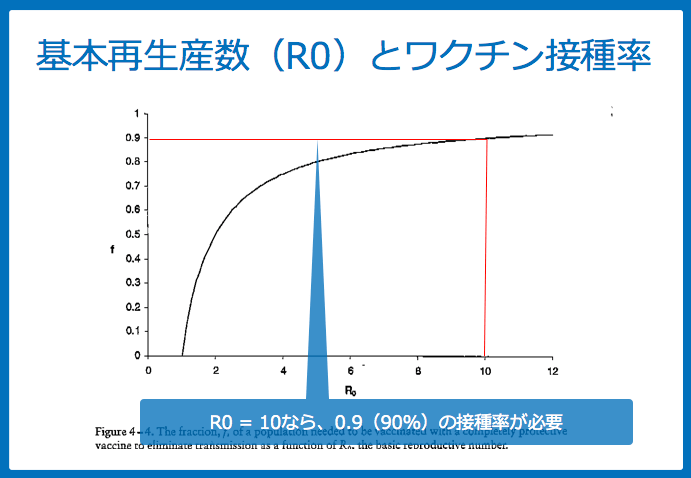
基本再生産数(R0)は目標とするワクチン接種率にも応用できます。
上の図は、X軸はR0、Y軸は f (ワクチン接種率)を表しています。
この母集団では、
- ワクチンの有効率は100%(打てば100%免疫がつく)
- 全員、免疫がない(Susceptible)
- 人の出入りが一切ない(Closed population)
- 人と人の接触はランダムかつ一定に起こる
という前提があるとしましょう。
この場合、R0 = 10の感染症の場合、ワクチン接種率はおよそ90%以上あれば、流行を防ぐことができます。
簡易式を用いる場合
f (目標とするワクチン接種率)は簡易的に計算することもできます。
- f = (1 – (1/R0))
です。例えば、先ほどのR0 = 10の感染症の場合、
- f = (1 – (1/R0)) = 0.9 = 90%
のワクチン接種率が必要となります。
まとめ
今回は感染症疫学の基本再生産数(R0)について説明してきました。
次回は実効再生産数(R)やS-I-Rモデルについて解説できればと思います。
続きはこちら↓↓