今回は遺伝疫学(genetic epidemiology)でよく行われるTwin Studyの研究手法について少し踏み込んで説明していこうとおもいます。
前回、Twin Studyの手法について表面的なことを解説しました。
- 双子の方に研究の参加をお願いする
- 一卵性or 二卵性を評価する
- 表現型(phenotype)を評価する
- 一卵性と二卵性双生児でのcorrelationやconcordanceを評価する
の順になります。
今回は、この最後の軽量的な評価、つまりcorrelationやconcordanceの評価や、heritabilityの評価について解説していければと思います。
オススメの教科書はこちらになります。遺伝疫学(genetic epidemiology)に興味のある方は、一読をお勧めします。
類似性(similarity)を評価する:
Measure of similarity
Twin studyでは最終的には類似性を評価するわけですが、具体的には
- Intraclass correlation coefficient
- Concordance rate
を使用します。
前者は連続変数(continuous variable)の場合に、後者は二項変数(dichotomous variable)の場合に使用します。
Intraclass correlation coefficientについて
まずはintraclass correlation coefficient (ri)について解説していきます。
Intraclass correlation coefficientを平たくいうと、双子同士のペアのアウトカムの相関係数(ri)を算出します。
例えば、双子の身長の相関をみたければ、
- 一卵性双生児同士の身長の相関係数(r1)
- 二卵性双生児同士の身長の相関係数(r0)
の2つを比較することになります。
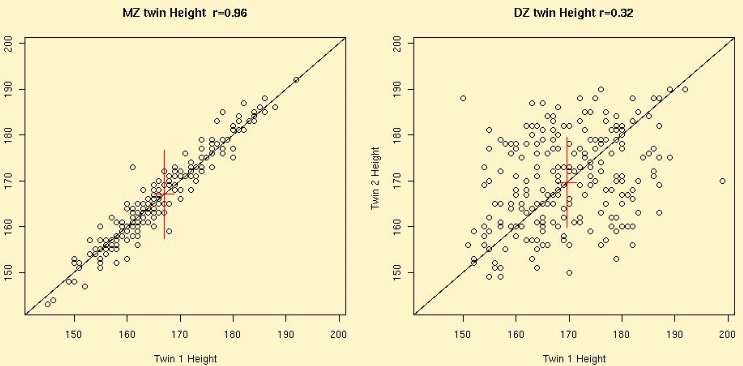 左の図が一卵性双生児の身長の相関係数ですが、r = 0.96となります。非常に似通っており、強い相関であるのがわかると思います。
左の図が一卵性双生児の身長の相関係数ですが、r = 0.96となります。非常に似通っており、強い相関であるのがわかると思います。
右の図は、二卵性双生児の身長の相関係数になります。r = 0.32と、一卵性双生児に比べると、弱い相関です。
相関係数を使用するので、rは0〜1の間になります。
1に近ければ、双子のペアは完璧に類似性のあることがしさされます。逆に、0に近ければそれぞれのペアの類似性は低く、ランダムに二人を抽出した場合と変わらないことをいいます。
Concordance rateについて
Concordance rateでは、ペアの片方(A1)がアウトカムを認めた場合(例:A病がある)、もう片方が(A2)同じ疾患を認める確率をいいます。
二人が一致している確率を計算するので、一致率(concordance rate)と呼ばれています。
表現型 = 遺伝 + 環境
Phenotype (P) = Genotype (G) + Environment (E)
ほとんどの疾患は遺伝的な要素(G)と環境的な要素(E)で決まることを留意する必要があります。
遺伝的な要素(Genotype)にも2つの種類があり、
- Additive genetics (A)
- Non-additive (dominance) genetics (D)
の2種類があります。
また、環境的な要素(Environment)には、
- Shared environment(C)
- Unique environmeet and measurement error (E)
の2つがあります。
Additive vs. Dominance Genetic Variation
まずはadditive genetic variationとdomestic genetic variationについて理解していきましょう。
Additive genetic variation (VA)
Additiveとは足し算のことをいいます。
例えば、とうもろこしの成長率が遺伝子1(A or a)と遺伝子2(B or b)によって決定されるとします。そして、
- A = 4 bu/ac
- a = 2 bu/ac
- B = 6 bu/ac
- b = 3 bu/ac
とします。
(*bu/acはbushles/acreの略でして、1acreあたり何bushles(1bu ≒35L)の穀物が育つのかの指標です)
AABBのgenotypeのとうもろこしはどうでしょうか?
Additive genetic variationでは、4 + 4 + 6 + 6 = 20 bu/acになります。Additive(足し算)ですよね?
AaBbのgenotypeの場合はどうでしょうか?
4 + 2 + 6 + 3 = 15 bu/ac となります。
このような考え方で計測されたvariationがadditive genetic varianceになります。
Dominance (non-additive) genetic variation (VD)
Dominance (non-additive) genetic variationの場合、どうなるでしょうか?
Dominanceの場合、遺伝子の強いほうに(A or aであれば、A)表現型が影響されます。このため、AABBでは4 + 4 + 6 + 6 = 20 bu/acになります。
また、AaBbでも、4 + 4 + 6 + 6 = 20bu/acになります。
このような考え方で計測されたvariationを、dominance genetic varianceといいます。
おまけ:Interactions between genes (VI)
じつはadditiveとdominance genetic variation以外にも、遺伝子同士の相互作用(interaction)を考慮する必要があります。
AAとBBの遺伝子が揃うと、足し算以上の効果がでたり、相殺しあってしまう場合にinteraction(相互作用)があるといいます。
今回の例でいうと、additiveやdominanceの場合はAABB = 20が理論値でしたが、AABB = 30 (>20)と出た場合などにinteractionを疑います。
Heritability analysis
Heritabilityとは、日本語で「遺伝率」などと呼ばれています。わりとラフに使われてしまっている場合もあります。
しかし、Heritabilityとは統計学的意味でして、基本的にはadditive polygenic modelに基づいて、疾患の表現型(P: phenotype)のばらつきが、遺伝子(G)と環境(E)に分けられることをいいます。
ここで、P, G, Eを使用して数式にすると、
P = μ+ G + E
となります。μは母集団での平均、Gは遺伝的な影響、Eは環境からの影響を指します。
Pの分散(ばらつき:variance)をみると、以下のようになります:
- (σP)2= (σG)2+ (σE)2
となります。ここでは、遺伝的な影響と環境からの影響は独立していると仮定しています。
ここでHeritability(H2)を定義すると、
H2= (σG)2/ (σP)2
となります。
この数式からわかるように、Heritability(H2)とは、疾患の表現型のばらつきのうち、遺伝子によるばらつきで説明される割合のことをいいます。Heritability(H2)は0〜1の間になります。
英語では「heritability is the proportion of variance in phenotype that is attributable to genetic influence」など解説されています。
Heritability(H2)の誤解
Heritability(H2)の意味をよく誤解されてしまっていることがあります。先ほども記載したとおり、Heritability(H2)とは、疾患の表現型のばらつきのうち、遺伝子によるばらつきで説明される割合のことです。
よくある解釈の間違いとして、
- 表現型が次の世代へ浸透する割合
- Heritabilityが高いほど、遺伝子が決定因子である
- Heritabilityが低いから、additive genetic varianceはない
- Heritabilityが高いから、遺伝子の影響が大きい
などがよくある誤解です。
例えばheritability = 0.7と計算された場合、「とある疾患(や特性)の70%が遺伝的な影響である」とは言えません。
集団における疾患のばらつきの70%が遺伝的な違いによるもの、という意味だからです。
GをさらにAとDで細分化する
ここで、genetic variability (G)をadditive (A) + dominance (D) variabilityに分けてみましょう。
先ほど説明したinteractionはないと仮定します。この場合、genetic variabilityは、
- (σG)2= (σA)2+ (σD)2
となります。
さらに、heritabilityは、
- H2= (σG)2/ (σP)2=((σA)2+ (σD)2)/ (σP)
となります。
Twin studyでHeritabilityを計測する方法
本題のtwin studyでheritabilityを計算する方法を考えてみましょう。twin studyでは、
- 一卵性双生児(MZ):遺伝情報は100%共有
- 二卵性双生児(DZ):遺伝情報は50%共有
と仮定をして計算していきます。
Additive effectのみの場合
次に、additive effectしかない(dominance effect = 0)と仮定をすると
- (σG)2= (σA)2
となります。
さらに、双子は同じ環境で暮らしていると考慮すると、双子間での共分散は、
- Cov(MZ) = 1.0(σA)2 + 0(σE)2
- Cov(MZ) = 0.5(σA)2 + 0(σE)2
となります。すると、
- 2[Cov(MZ) – Cov(DZ)] = (σA)2
となります。そして最終的に、
- H2= (σA)2/ (σP)2
となります。
ACE modelについて
ACE modelのACEそれぞれは、
- A: additive genetic effect
- C: common or shared environmental effects
- E: unique or non-shared environment for co-twins
となります。この場合、分母のPは、
- (σP)2= (σA)2+ (σC)2+ (σE)2
となります。
Intraclass correlationの値がわかっている場合
Intraclass correlation(rMZやrDZ)の値がわかっている場合、以下の等式を使用することができます:
- h2(ACE) = 2(rMZ– rDZ)
例えばこちらのデータを見てみましょう(Silventoinen et al., 2003):
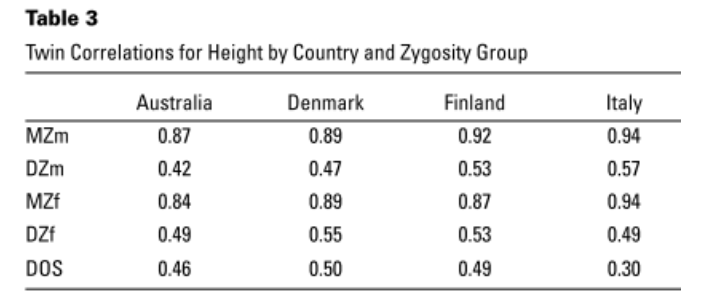
オーストラリアの男女における身長のheritabilityを計算すると、
- 男性: 2x(0.87 – 0.42) = 0.90
- 女性: 2x(0.84 – 0.49) = 0.70
となります。
デンマークの男女における身長のheritabilityを計算すると、
- 男性: 2x(0.89 – 0.47) = 0.84
- 女性: 2x(0.89 – 0.55) = 0.68
となります。
Intraclass correlationsを使用した上のheritabilityの計算は、近年は使用されなくなってきている
この公式は2000年代中盤くらいまではよく利用されていましたが、近年は使用されなくなってきています。
統計や疫学手法が近年画期的に進歩しています。例えばGWASからheritabilityを推定する際には、LD score regression (LDSR)など、様々な手法が使用されています(Czajkowski et al., 2018; Suggs et al., 2018)。
最後に
今回はTwin studyにおけるconcordance, intraclass correlationや、heritabilityについて解説してきました。
次回は、Faimily studyについて解説できればと思います。
参考文献
- Czajkowski, N., Aggen, S. H., Krueger, R. F., Kendler, K. S., Neale, M. C., Knudsen, G. P., … Reichborn-Kjennerud, T. (2018). A Twin Study of Normative Personality and DSM-IV Personality Disorder Criterion Counts: Evidence for Separate Genetic Influences. The American Journal of Psychiatry, 175(7), 649–656. https://doi.org/10.1176/appi.ajp.2017.17050493
- Silventoinen, K., Sammalisto, S., Perola, M., Boomsma, D. I., Cornes, B. K., Davis, C., … Kaprio, J. (2003). Heritability of adult body height: a comparative study of twin cohorts in eight countries. Twin Research : The Official Journal of the International Society for Twin Studies, 6(5), 399–408. https://doi.org/10.1375/136905203770326402
- Suggs, A., Loesch, M., Ezaldein, H., Christensen, L., Dawes, D., & Baron, E. (2018). An Acne Survey from the World’s Largest Annual Gathering of Twins. Journal of Drugs in Dermatology : JDD, 17(4), 380–382. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/29601613