遺伝的連鎖、組み換えを理解して連鎖不平衡の指標を計算する [遺伝疫学]

今回は、

• Genetic linkage（遺伝的連鎖）
• Recombination（組み換え）
• Identity by descent (IBD：同祖対立遺伝子)
• Linkage disqeuilibriumの計算方法

などを具体的に説明していきます。

前回は、遺伝疫学で重要なメンデルの法則と、Herdy-Weinbergの法則について、遺伝疫学的な視点から解説してきました。

Familial Aggregation Studyについて：遺伝疫学（Genetic Epidemiology）今回は遺伝疫学（genetic epidemiology）でよく行われるFamilial Aggregation Studyの研究につい...

遺伝疫学について、少し詳しく知りたい方は、こちらは基礎知識として理解しておいたほうが良い内容と思います。

Genetic Linkageとは？

Genetic linkage（遺伝的連鎖）とは、特定の対立遺伝子の組み合わせが、メンデルの独立の法則に従わずに、親から子へ一緒に遺伝する遺伝学的現象のことを言います。

このgenetic linkageと遺伝疫学を結びつけて考える前に、まずは配偶子の組み換え(recombination)について理解しましょう。

配偶子の組み換え（recombination）について

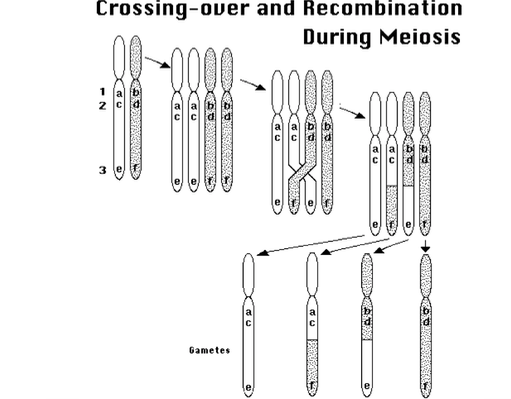
配偶子は減数分裂の際に、乗り越えcrossing-over（３つ目の図）をし、遺伝子の組み換え（recombination）をします。

この図からもう１つわかることは、距離とrecombinationについてです。
例えば、a-cやb-dは距離的に近いので、recombinationを起こす確率が少ないです。一方で、a-eやb-fは距離が遠いため、recombinationを起こす確率が高いと言えます。

つまり何が言いたいかというと、同じ染色体の場合、メンデルの提唱した「独立の法則」は成立しない可能性があります。さらに、その可能性は対象とする遺伝子同士の距離にもよります。

この特徴を利用した解析でLOD score linkage analysisがありますが、こちらはまたの次回に詳しく説明します。

Linkageの例

少しだけ簡単な例を考えてみましょう。まずは以下の図を見てください。

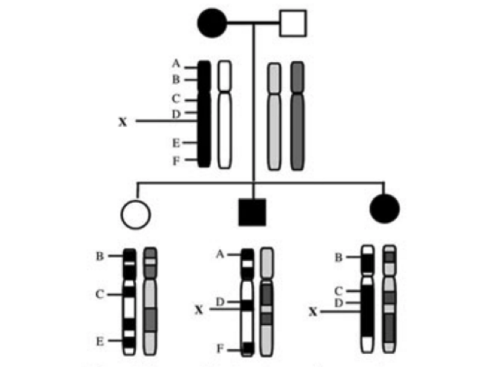
この家族では、母親が常染色体優性遺伝疾患の罹患者だったとします。
疑われている遺伝子はA〜Fの６箇所がありました。Xは遺伝子のマーカーで、この部分を染色体上で目印をつけることができたとします。

ここで、Xの情報しかわからない状況とします。つまり、

• 左の子：Xなし、疾患なし
• 中の子：Xあり、疾患あり
• 右の子：Xあり、疾患あり

A〜Fの遺伝子のうち、どれがもっとも可能性として高いでしょうか？

この情報を見ると、Xと疾患ありは関連していそうな印象を受けます。

そこで、Xと遺伝的な距離が近いのはDで、Linkageが強いと考えられるため、D周辺が原因遺伝子の位置としてもっとも怪しそうな印象を受けます。

Identity by descent (IBD)という概念

Identity by descent (IBD)は同祖対立遺伝子と呼ばれています。

IBDとは2個体間で対立遺伝子が祖先の同じものを共有する（これを同祖であるという）状態をいい、０〜２で表すことができます。

IBDの例

例えば以下の図を見てみましょう。

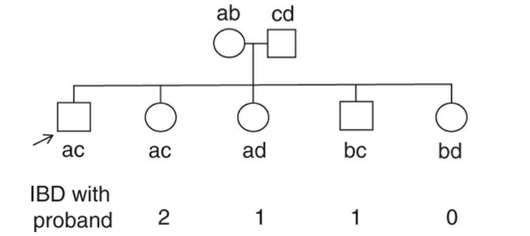
父親がab、母親がcdの遺伝子を持っていたとします。
今回の発端者を一番左（Proband）とすると、左から順にIBDは2, 1, 1, 0となります。
つまり、発端者の遺伝子acのうち、全て一緒なら２を、a or cの１つだけなら１を、aもcもなければ０となります。

Linkage disequilibrium (連鎖不平衡) について

Linkage disequilibrium (連鎖不平衡)とは生物の集団において、複数の遺伝子座の対立遺伝子または遺伝的マーカーの間にランダムでない相関が見られる、すなわちそれらの特定の組合せの頻度が有意に高くなる集団遺伝学的な現象をいいます。

先ほども少し説明しましたが、Linkage disequilibrium (LD)は同じ染色体上の近しい遺伝子同士の場合、より起こりやすい傾向にあります。

Linkage disequilibrium (LD)の計算方法

Linkage disequilibrium (LD)を計算する方法を、順に説明していきます。
例えば、AaとBbというheterozygoteの遺伝子型を考えてみましょう。
この場合、あり得る組み合わせとしては、

• AB とab
• AbとaB

のいずれかになります。

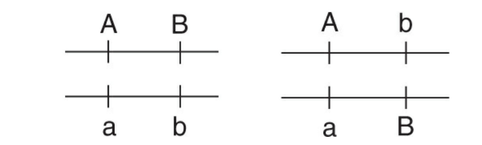
この時に、LDがあるかどうかを判断するには、ABの頻度、Aのみの頻度、Bのみの頻度の３つを計算するとわかります：

• f(A-B)
• f(A)
• f(B)

そして、f(A-B)とf(A) x f(B)を比較して、

• f(A-B) = f(A) x f(B) ：LDの可能性は低い（独立している）
• f(A-B) ≠f(A) x f(B)：LDの可能性がある（独立していない）

となります。

LDを計測する

LDの大きさを計算するには、まず

• D = f(A-B) – f(A) x f(B)

を計算します。

しかし、この値はマイナスになる可能性もあるため、次に以下を計算します。

• D_max= Minumum[f(A) x f(b), f(a) x f(B)]

つまり、ここではf(A) x f(b)またはf(a) x f(B)で小さい方をD_maxとします。

さらに、DをD_maxで割、さらに絶対値を取ります：

• D’ = |D / D_max|

これがLDの計測値となります。

さらに、tag SNPsなどがある場合、相関(r²) を計算することがあり、これは

• r²＝D²/[f(A) x f(a) x f(B) x f(b)]

となります。

LDの計算例

以下の例を見てみましょう。

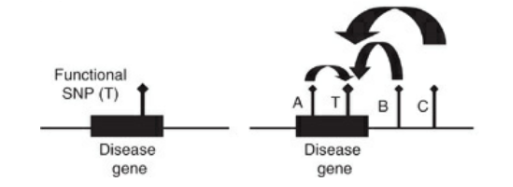
今回の研究では、SNP Tを探索する研究としましょう。
現時点で、A, B, CというSNP上または周囲の遺伝子型が分かっていたとします。

Aは疾患遺伝子上にはありますが、疾患に関わる機能はなかったとします。BとCは疾患遺伝子上にはなく、単に同じ染色体上の遺伝子とします。

ここで、A以下の４つのhaplotypeが判明したとします（簡略のため４つとなっています。理論上は16タイプあります）。

これをもとに、LDを計算してみましょう。

まず、f(A), f(B), f(C)を計算します。Frequencyを見ていただければわかりますが、

• f(A) = 0.3
• f(B) = 0.3 + 0.4 = 0.7
• f(C) = 0.3 + 0.4 + 0.2 = 0.9

となります。このため、

• f(a) = 0.7
• f(b) = 0.3
• f(c) = 0.1

となります。

次にhaplotypeを見ると、Aの時は疾患があり（T）、aの時は疾患がないため(t)、Tおよびtの確率はAと等しくなり

• f(T) = 0.3
• f(t) = 0.7

となります。

ここで、TとBのLDを計算すると、

• f(T–B) = 0.3
• D = f(T–B) – f(T) x f(B) = 0.3 – 0.3*0.7 = 0.09
• D_max= min[f(T) x f(B), f(t) x f(B)] = min[0.09, 0.49] = 0.09
• D’ = |D/ D_max| = 0.09/0.09 = 1
• r²= D²/[f(T) x f(t) x f(B) x f(b)] = 0.18

となります。

以上を繰り返すと、以下のような表になります：

	D	D’	r2
A	0.21	1.00	1.00
B	0.09	1.00	0.18
C	0.03	1.00	0.05

AはD’もr²も1.00であるため、perfect LDと判断します。

おわりに

今回はcross-overとrecombinationの説明から始まり、この現象をgenetic epidemiologyではLDの計算にどう活かしているのかを簡単に説明してきました。

次回はLinkage analysisという実際の解析方法について、少しずつ解説していければと思います。

遺伝疫学について、詳しく知りたい方は以下の本をお勧めします：