前回はCausal Mediation Analysisの概念や記載方法、前提条件について記載してきました。
https://www.dr-kid.net/causal-mediation
今回は、実際に治療(X)、媒介因子(M)、アウトカム(Y)をどのように分解して考えるのか(以下、Decomposition)を記載していきます。
Decompositionにも様々な種類がありますが、大きく分けて
- 2-way decomposition
- 3-way decomposition
- 4-way decomposition
の3種類に分けられます。
基本は4-way decompositionを覚えて、それを3-wayや2-wayに応用していくのが一番スムーズですが、最初にdecompositionをどのように行われてきたのかを説明するために、2-way decompositionを例に解説していきます。
Causal Mediation Analysisを本格的に勉強したいかたは、以下の書籍が必読です↓
(2025/05/11 12:39:11時点 Amazon調べ-詳細)
Decompositionとは?
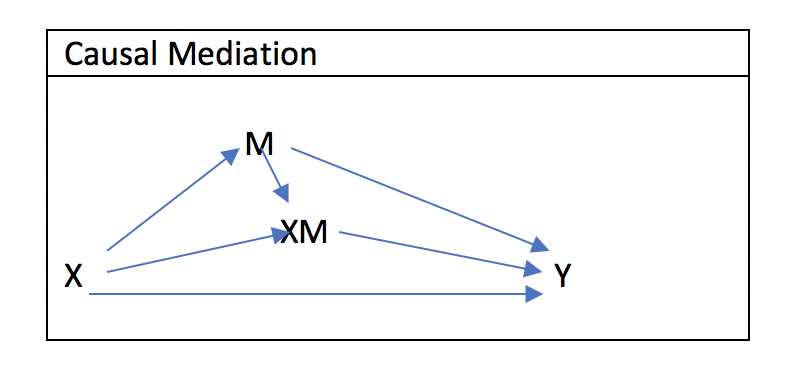
Decompositionとは、治療(X)がアウトカム(Y)に与える影響を、媒介因子(M)を介しているか、いないかで分けることを意味します。
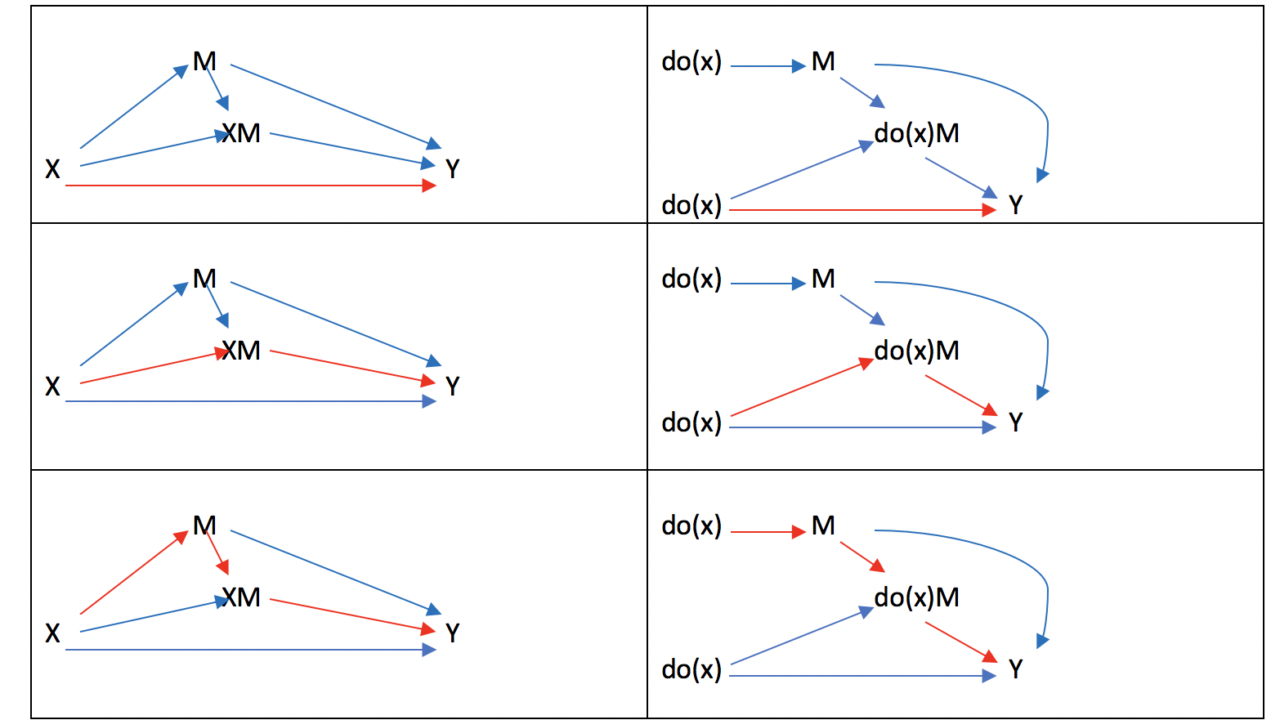
例えば、上のAugmented DAGの経路は4通りありますが、以下のように2-way decompositionを行えます。
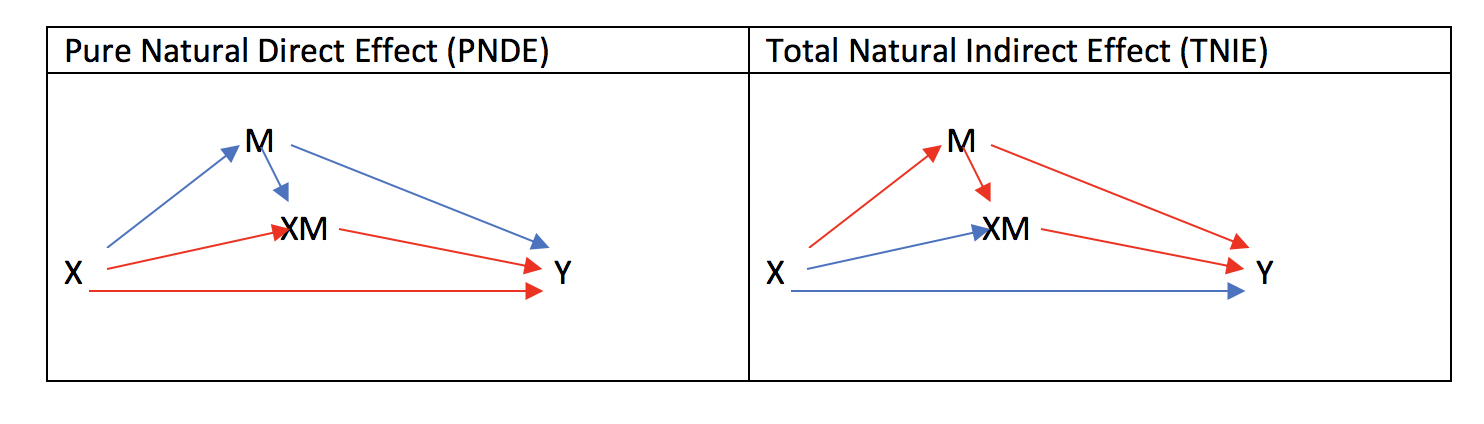 赤色の経路が見たい治療効果です。
赤色の経路が見たい治療効果です。
Two-way decompositionを数式として理解する
前回、4つのnested counterfactualを解説しました。
YxMxとYxMx*とYx*MxとYx*Mx*でしたね。
これを利用しつつ、このtwo-way decompositionを考えてみましょう。
まず、XがYに与える効果は、Potential outcomeのフレームワークでは、以下の通りでした。
- E(Yx) – E(Yx*)
これをNested counterfactualにすると、consistencyからYx= YxMxとなるため、
- E(Yx) – E(Yx*) = E(YxMx) – (Yx*Mx*)
となります。
さらに、ここのE(YxMx*) – E(YxMx*) (つまり0)を代入すると、
- E(YxMx) – (Yx*Mx*)
= E(YxMx) – E(Yx*Mx*) + E(YxMx*) – E(YxMx*)
= E(YxMx) – E(YxMx*) + E(YxMx*) – E(Yx*Mx*)
= TNIE + PNDE
とTotal Natural Indirect Effect + Pure Natural Direct Effectのように分解できます。
つまり、nested counterfactualを入れることで、XからYに与える影響を2つのパートに分解できてしまったのです。これをtwo-way decompositionと呼んでいます。
Two-way decompositionの別の例:E(Yx*Mx) – E(Yx*Mx) を代入
次に、E(Yx*Mx) – E(Yx*Mx) をPotential outcomeに代入して考えてみましょう。
- E(Yx) – E(Yx*)
- = E(YxMx) – E(Yx*Mx*)
- = E(YxMx) – E(Yx*Mx*) + E(Yx*Mx) – E(Yx*Mx)
- = E(YxMx) – E(Yx*Mx) + E(Yx*Mx) – (Yx*Mx*)
- = TNDE + PNIE
と、Total Natural Direct Effect (TNDE)とPure Natural Indirect Effect (PNIE)の2つに分けられます。
これをAugmented DAGで表現すると以下のようになります。
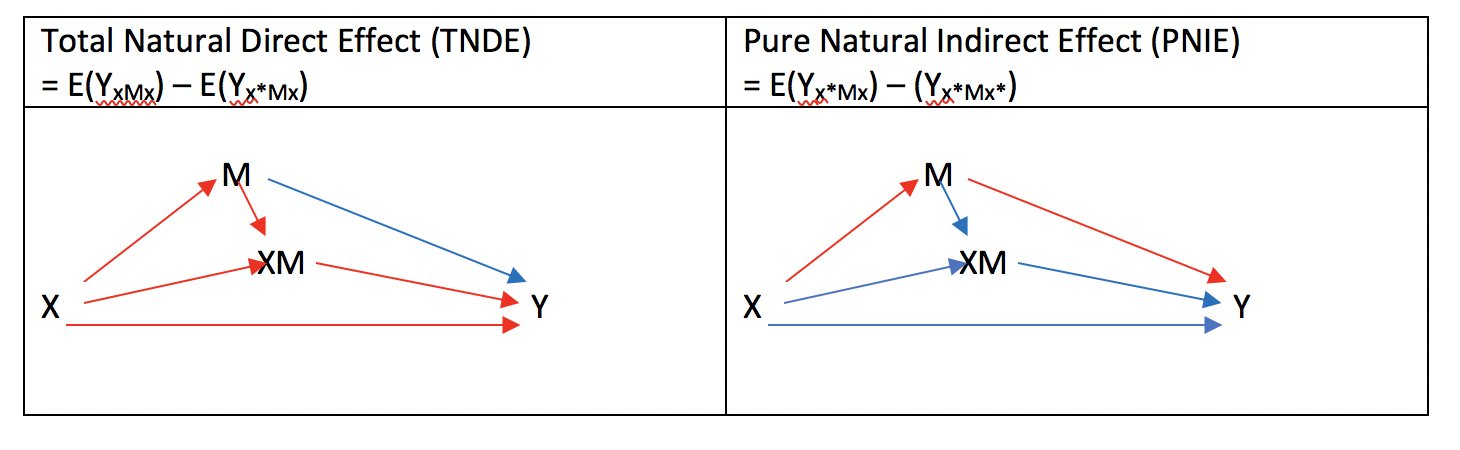
さらにここから、Total Natural Direct Effect (TNDE)が何をみているのか、Augmented DAGを利用して考えてみましょう。
E(YxMx)の赤色のパートは、XがMを介さずにYに与える影響でした。一方で、E(YxMx)の赤部分は、XがMを介してYに与える影響です。
これをDAG上で表すと、E(YxMx)とE(Yx*Mx)はそれぞれ以下のようになります。
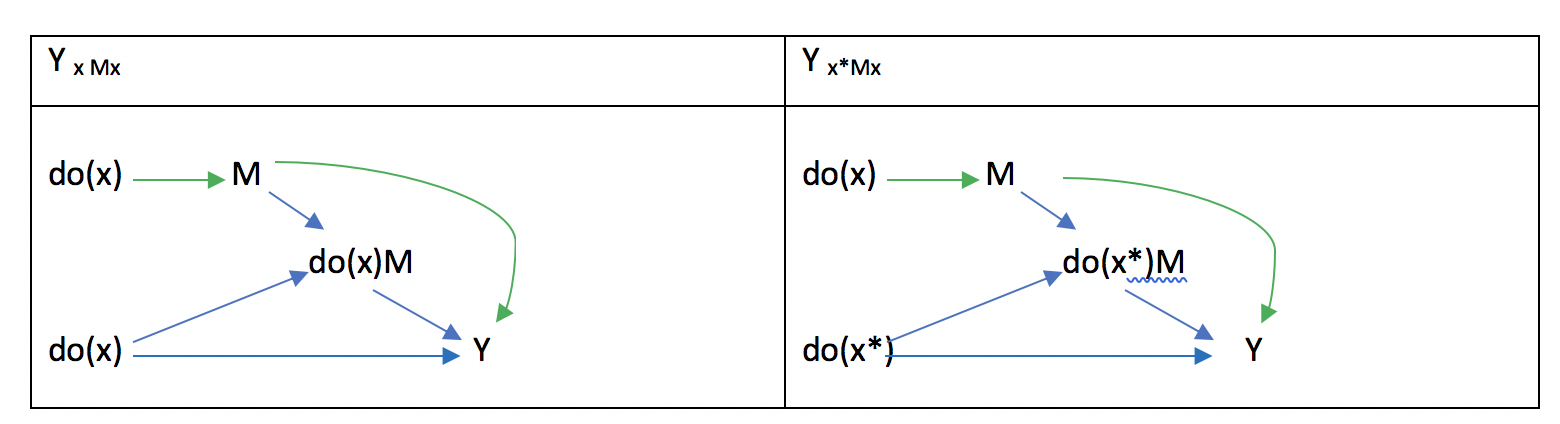
緑で記した矢印の経路は、do(x)→M→Yで、左右どちらも一緒のため、相殺されて消えてしまいます。
一方で、残りの3つのパートは左と右で異なるため、治療効果として計測できます。
具体的には、
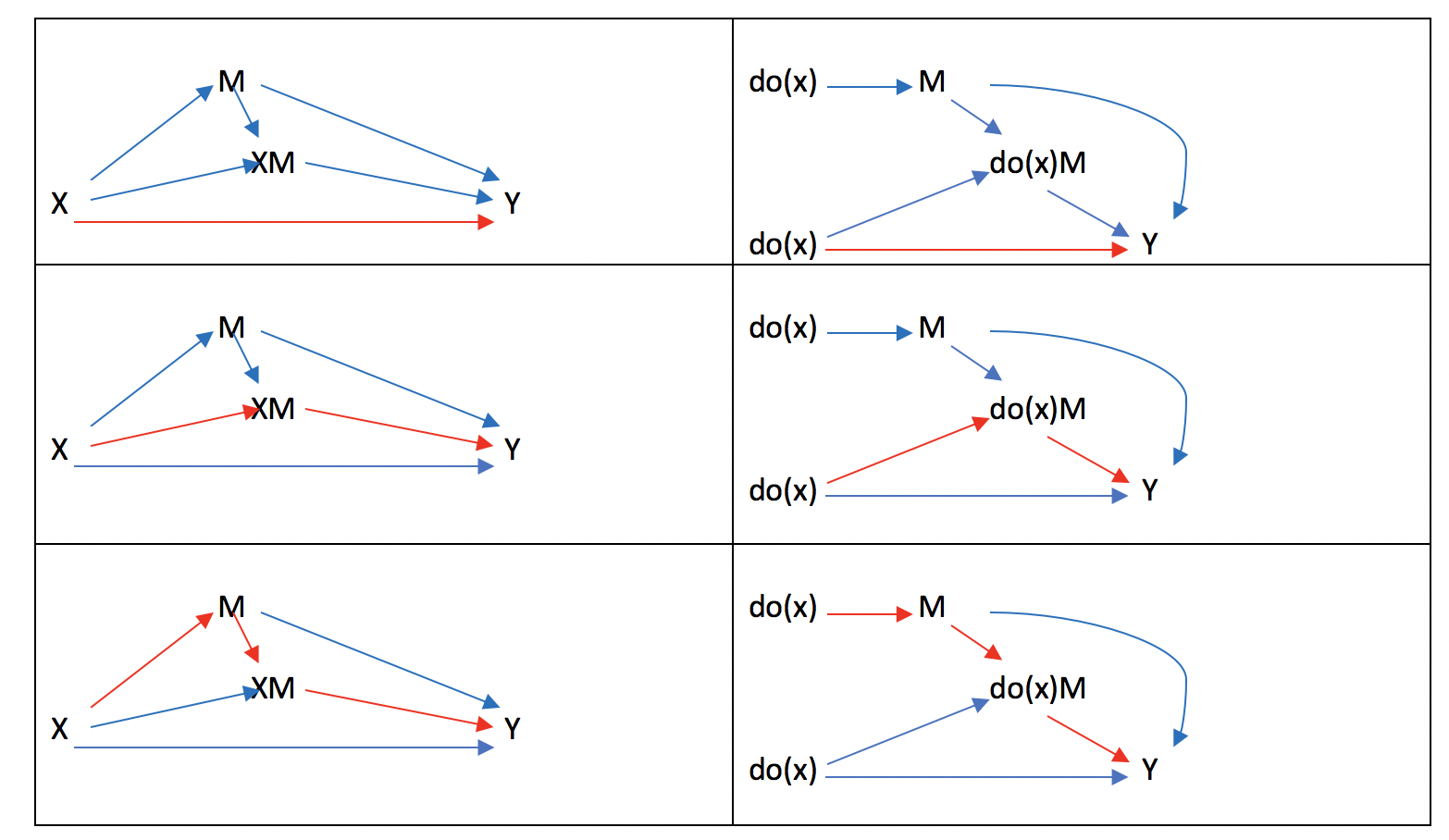
のように、3つの経路を足して計測していたことになります。
4-way decompositionについて
Causal Mediation Analysisの基本は4-way decompositionです。
治療がアウトカムに与える影響を4つにdecompositionできれば、あとはそれの組み合わせを考えて、3-wayや2-way decompositionにすれば良いからです。
4-way decompositionは以下のような構成になります。
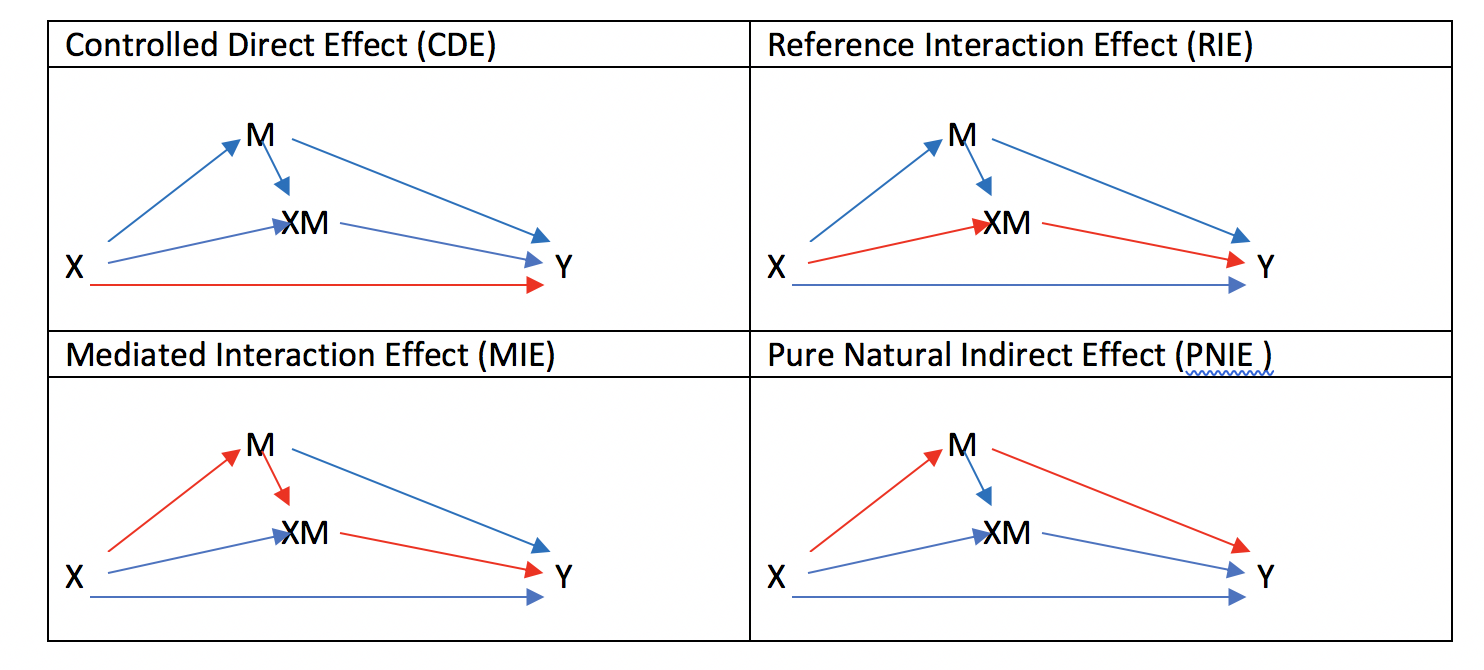
まず上の4-way decompositionについて解説する前に、mediationとinteractionについてみてみましょう。
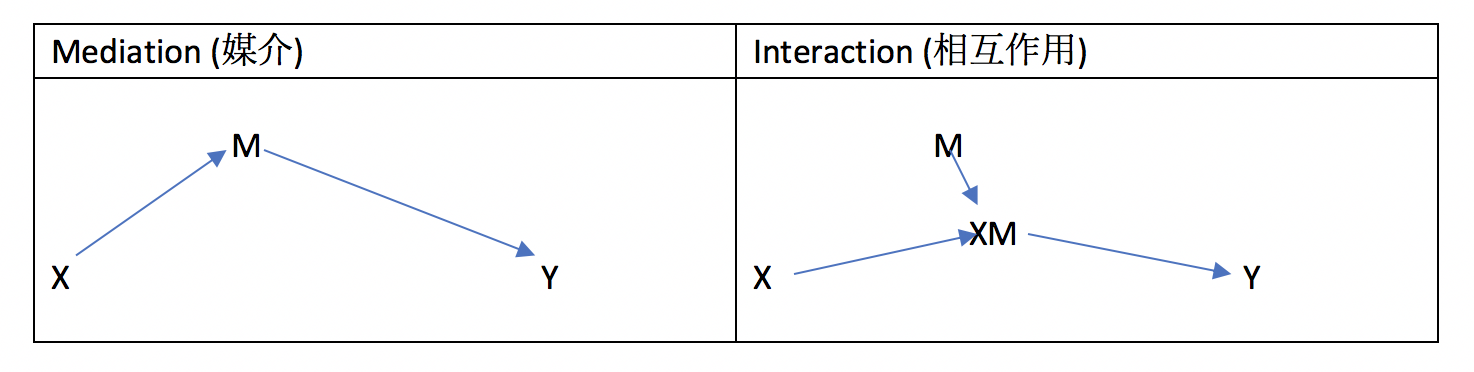
Mediationとは、治療(X)が媒介因子(M)を介してYに与える効果でした。
Interactionとは、治療(X)が媒介因子(M)と重なりあう効果、つまり相互作用をいいます。4-way decompositionではこの2つのある/なしで、4つに分けて考えると分かりやすいでしょう。
|
|
Mediation |
Interaction |
|
CDE |
なし |
なし |
|
RIE |
なし |
あり |
|
MIE |
あり |
あり |
|
PNIE |
あり |
なし |
Controlled Direct Effect (CDE)について
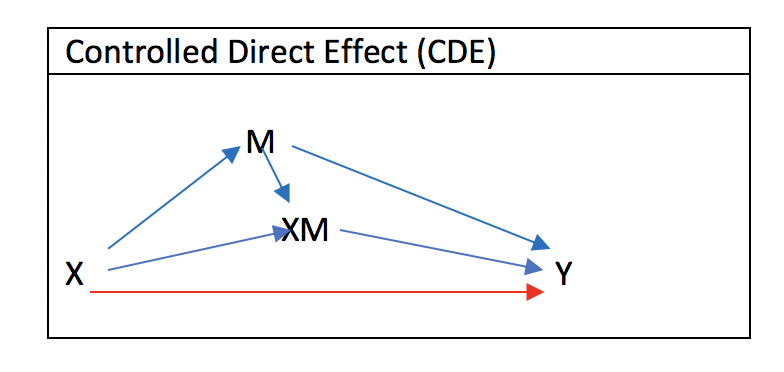
Controlled Direct Effect (CDE)は、MediationもInteractionも介さない、直接経路でした。
“Controlled”と言われる所以は、媒介因子(M)をM = m*に固定するからです。
これをPotential Outcomeのフレームワークで記載すると、
- E(Yxm*) – E(Yx*m*)
となります。
ここではnested counterfactual (YxMx)の表記は必要ありません。なぜなら、いかなるXの値でもM = m*と固定してしまうからです。
Reference Interaction Effect (RIE)について
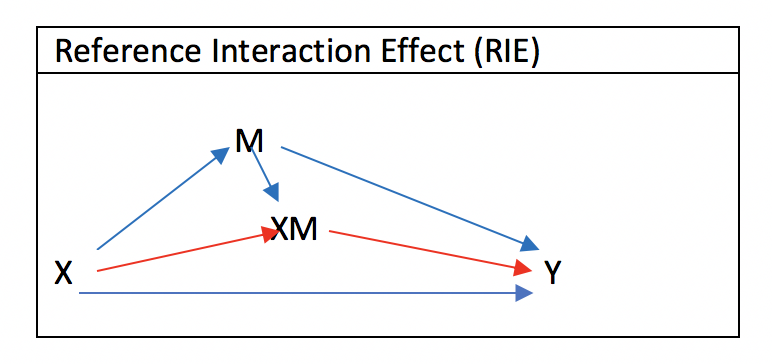
Reference Interaction Effect (RIE)をaugmented DAGで表現すると以上の通りでした。
よくよく考えてみると、先ほど紹介したNatural Direct EffectとControlled Direct Effectの差を取れば求められるのが分かります。
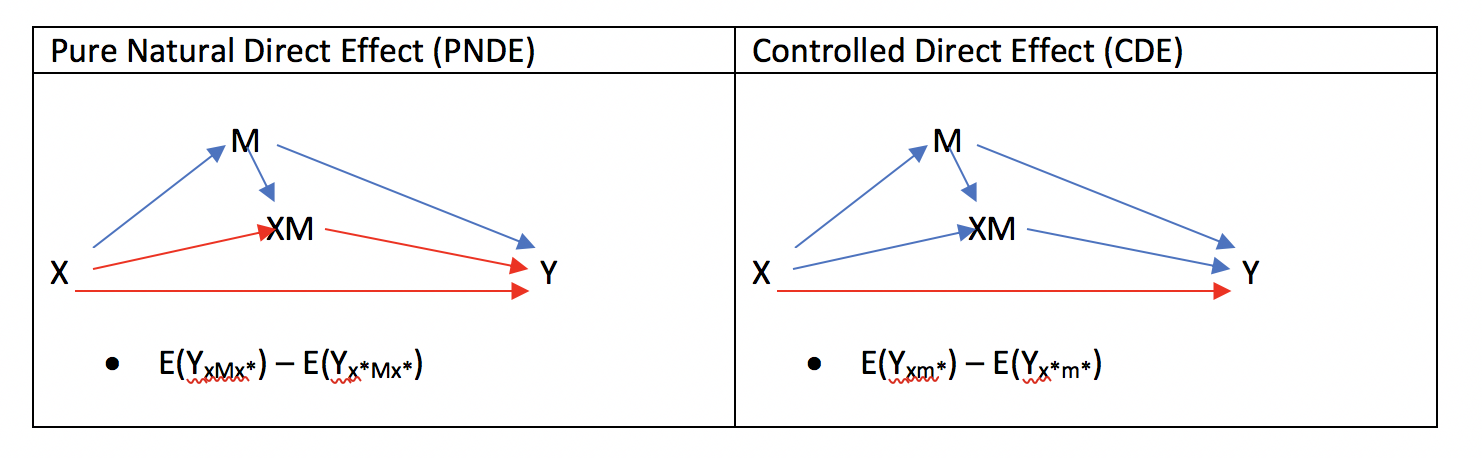
よって、RIEは以下のようになります。
- RIE
- = PNDE – CDE
- = [E(YxMx*) – E(Yx*Mx*)] – [E(Yxm*) – E(Yx*m*)]
Mediated Interaction Effect (MIE)について
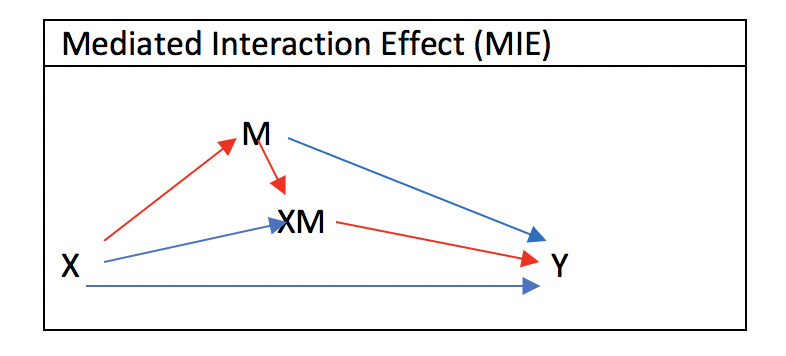
Mediated Interaction Effect (MIE)も同じような考え方で、Total Natural Direct Effect (TNDE)から、Pure Natural Direct Effect (PNDE)の差を取ってしまえば計測できます。
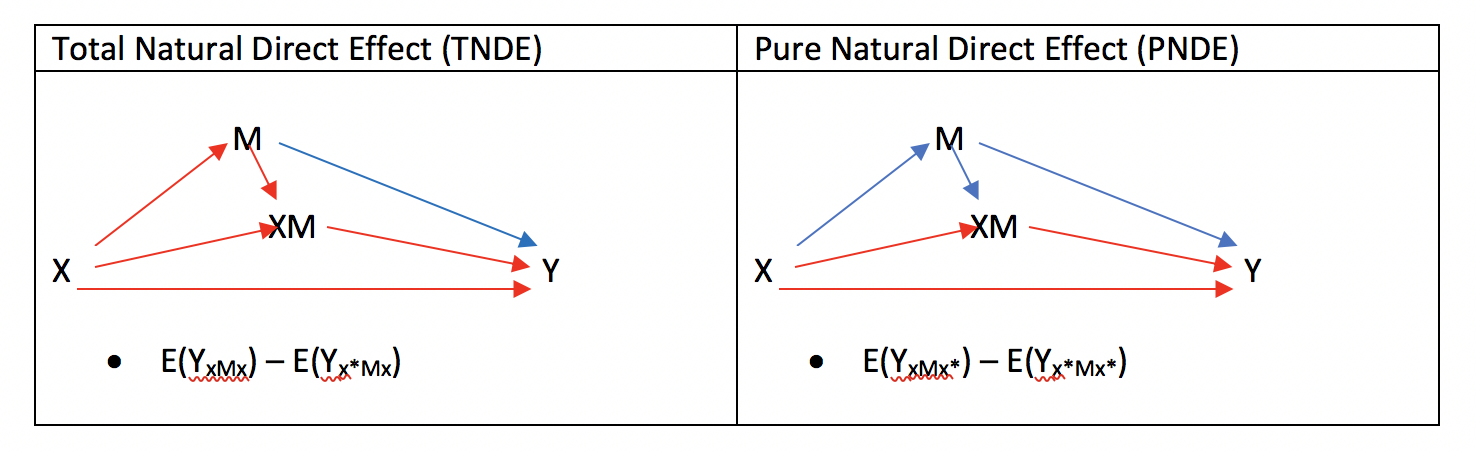
よって、
- MIE
- = TNDE – PNDE
- = [E(YxMx) – E(Yx*Mx)] – [E(YxMx*) – E(Yx*Mx*)]
となります。
Pure Natural Indirect Effectについて
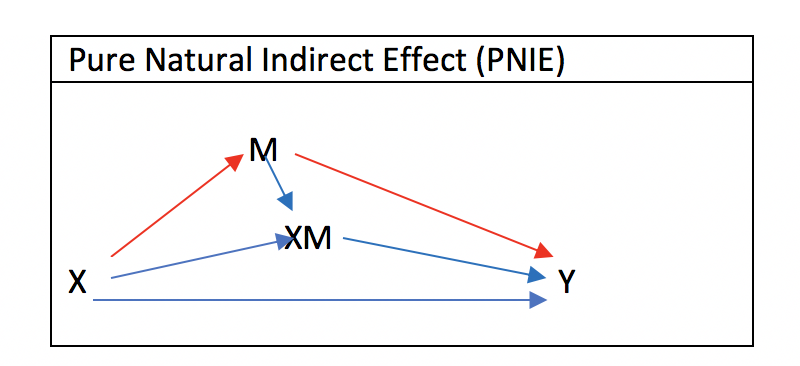
Pure Natural Indirect Effect(PNIE)も同様に、Total EffectからTotal Natural Direct Effect (TNDE)の差をとることで計算できます。
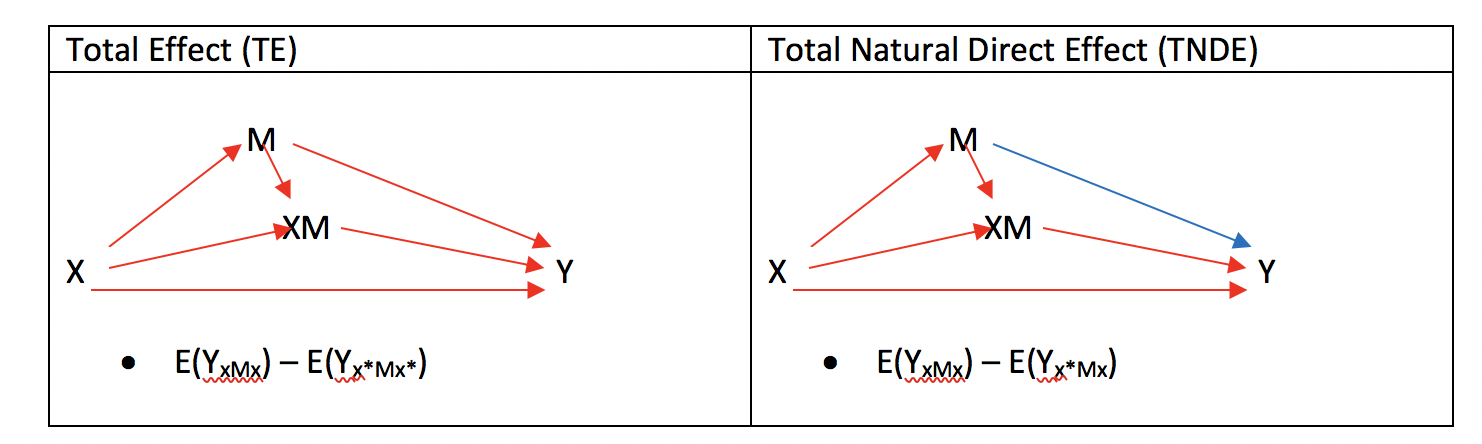
よって、以下のような数式になります。
- PNIE
- = TE – TNDE
- = [E(YxMx) – E(Yx*Mx*)] – [E(YxMx) – E(Yx*Mx)]
- = E(Yx*Mx) – E(Yx*Mx*)
以下、Potential Outcomeでの数式をまとめた表です。
|
CDE |
E(Yxm*) – E(Yx*m*) |
|
RIE |
[E(YxMx*) – E(Yx*Mx*)] – [E(Yxm*) – E(Yx*m*)] |
|
MIE |
[E(YxMx) – E(Yx*Mx)] – [E(YxMx*) – E(Yx*Mx*)] |
|
PNIE |
E(Yx*Mx) – E(Yx*Mx*) |
RIEやMIEは4つのnested counterfactualを使用している点に疑問を覚えた方がいるかもしれません。
ですが、普通に考えてみて、相互作用(Interaction)をみるには、差の差を取らなければ見れないことを思い出していただければ納得いくと思います。
3-way decompositionについて
3-way decompositionでは、4つある経路を3に分ける作業です。
ですので、4-way decompositionで手に入れた数式を、そのまま組み合わせるだけで計測可能です。
TE = CDE + PAI + PNIEの場合
Total EffectをCDEとPNIEと残りに分ける場合です。
この場合、Portion Attributable Interaction (PAI) = RIE + MIEとなります。
DAGで表現すると以下のようになります。
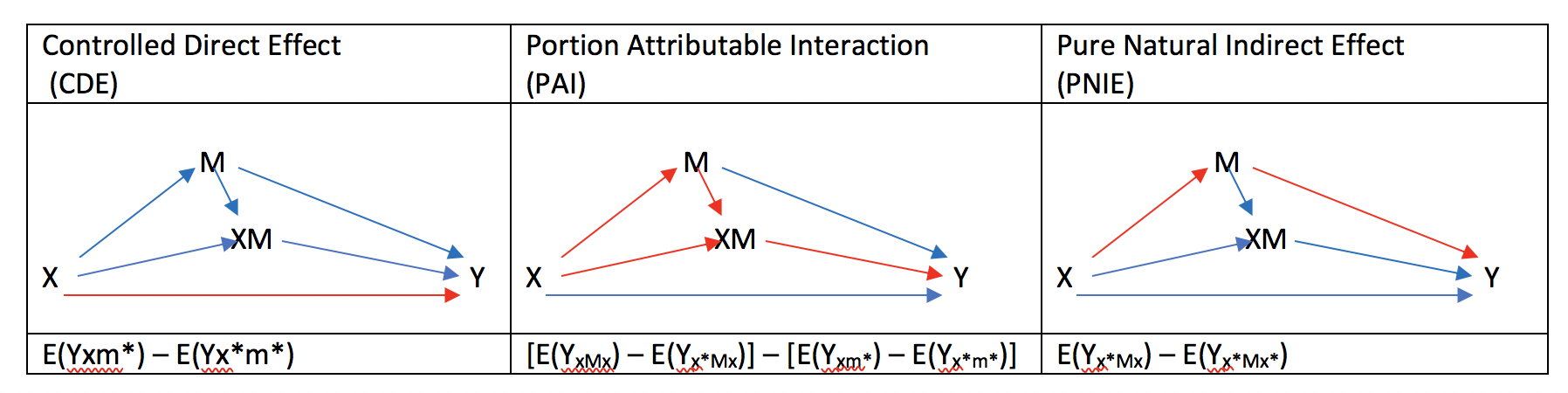
TE = PDE + MIE + PNIEの場合
次は、TEをPure direct effect + MIE + PNIEに分ける場合をみてみましょう。
この場合、Pure Direct Effect = CDE + RIEとなります。
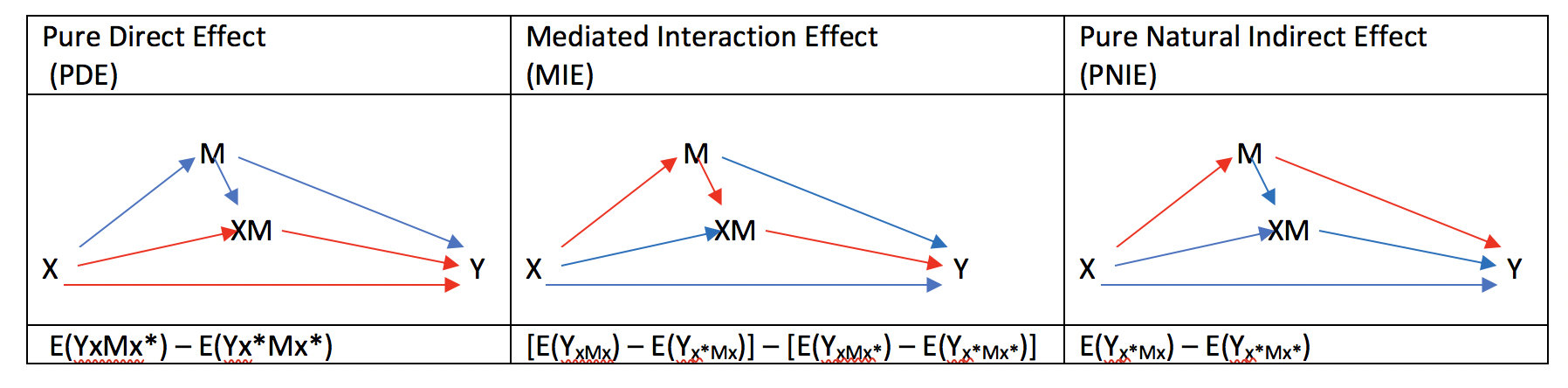
TE = CDE + RIE + TNIEの場合
3-way decompositionの最後に、Total EffectをCDEとRIEとTNIEに分けた場合です。この場合、Total Natural Indirect Effect (TNIE) = MIE + PNIEとなります。
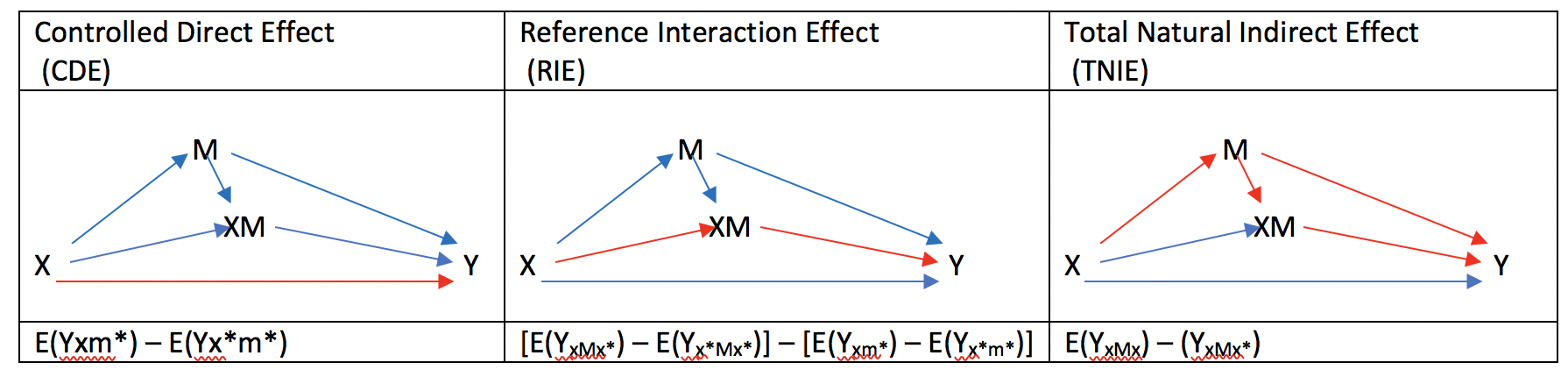
2-way decompositionについて
2-way decompositionは最初に説明してきたので、少し省略しますが、以下の3パターンがあります。
TE = PNDE + TNIE
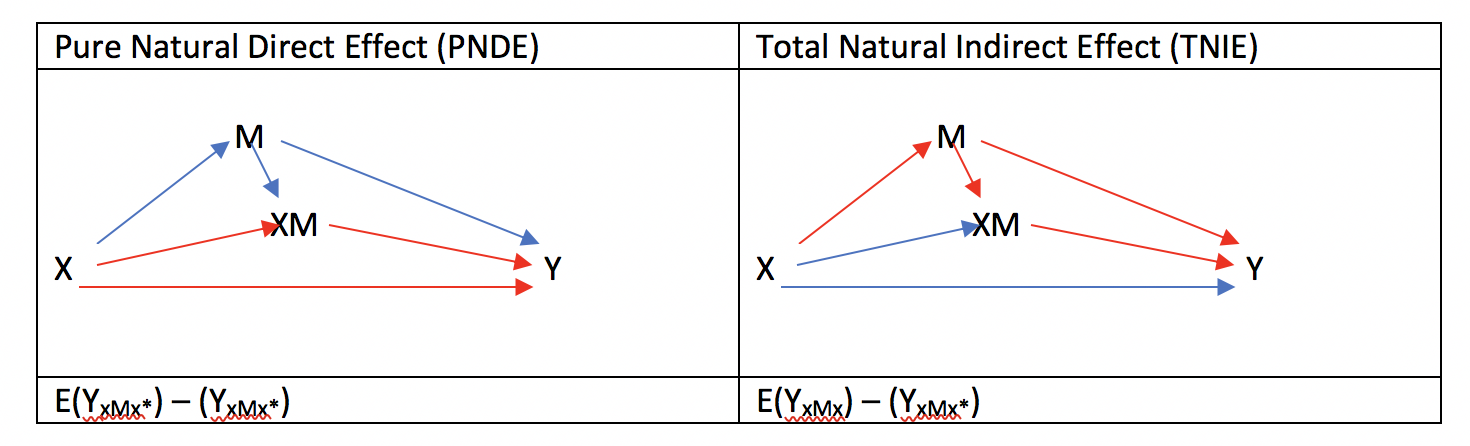
TE = TNDE + PNIE
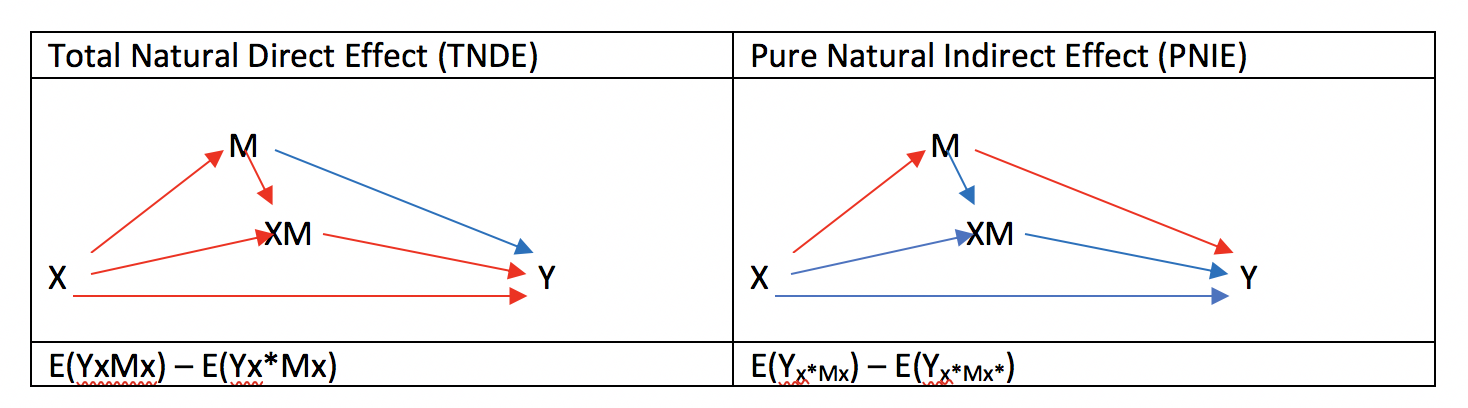
TE = CDE + PE
PEはportion eliminatedを意味します。CDEというportionを除外した(eliminated)からportion eliminatedです。
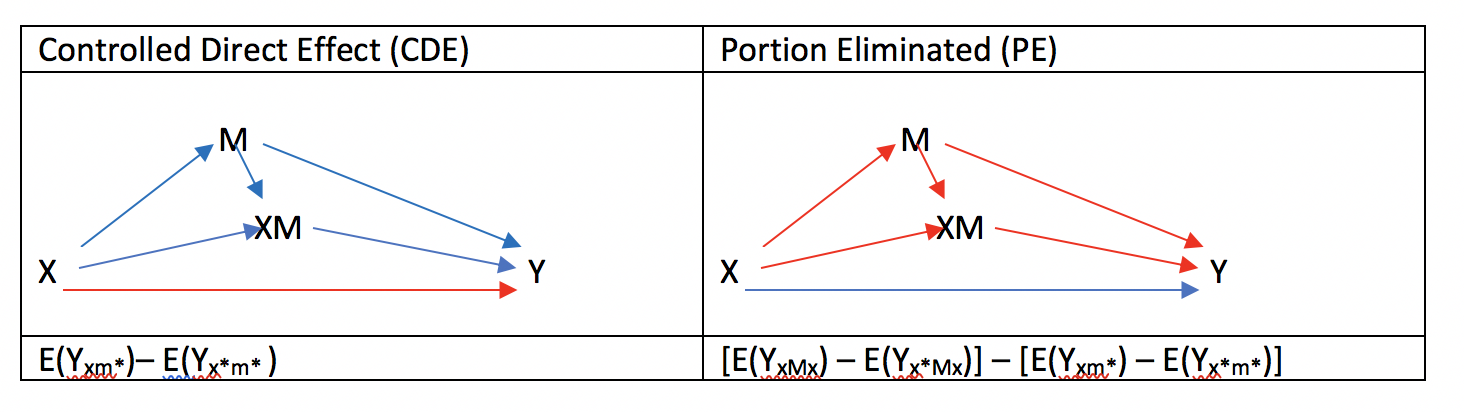
それぞれの効果の名前について:”Natural”, “Direct/Indirect”, “Total”
- Natural
- Direct/Indirect
- Total
など、いろんな名前が混ざっていて覚えづらいと思う方がいるかもしれません。
私も最初にCausal Mediation Analysisを勉強した際にはそうでした。
ですが、語源を少し理解すると、簡単にイメージできるようにできます。
以下のように表にすると分かりやすいです
|
|
Direct |
Indirect |
|
|
YxMx |
YxMx |
|
Natural |
PNDE |
PNIE |
|
Total |
TNDE |
TNIE |
例えば、”Direct”と記載されている場合は、YxMxのうち赤色の部分に興味があります。このため、YxMxとYx*Mxを比較することになります。
次に、Mxに注目して、naturalであればMx*を、totalであればMxを入れれば数式が出来上がります。
“Indirect”の場合は、この逆を行います。
Indirect effectで興味はあるのは、YxMxの赤色の部分です。
よって、YxMxとYxMx*の比較になります。
そして、次にYxに注目し、naturalがつけばYx*を、totalであればYxを入れれば数式が成り立ちます。
名前はややこしいですが、なぜこのように呼ばれているのか、語源を考えることで、全て暗記しなくても覚えることができます。
まとめ
今回は、Causal Mediation Analysesに置ける3つのdecomposition
- 4-way decomposition
- 3-way decomposition
- 2-way decomposition
について解説してきました。
また、”direct/indirect “や”natural/total”の語源についても追加で解説しています。
次回は、これらのpotential outcomeのフレームワークを抜け出して、実際にどのように計算するのか、g-formulaやregressionでのempirical analogueを説明していきます。
(2025/05/11 12:39:11時点 Amazon調べ-詳細)