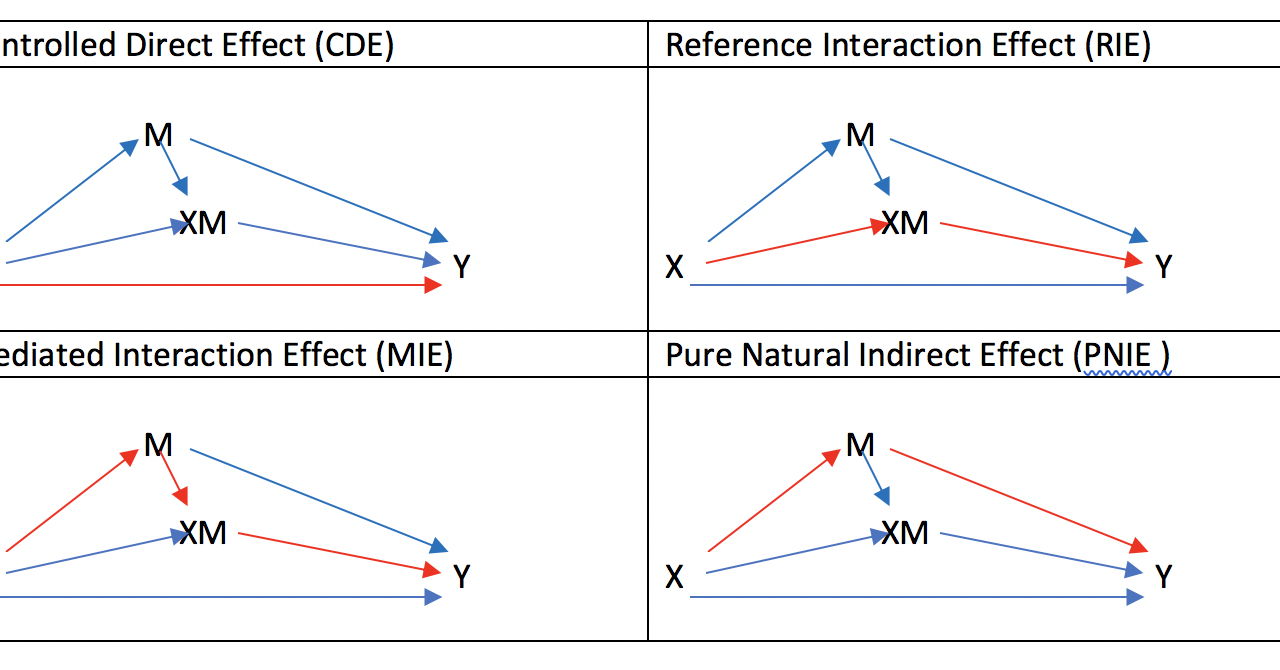
前回はCausal Mediation Analysisにおいて、2-way / 3-way / 4-way decompositionについて解説してきました。
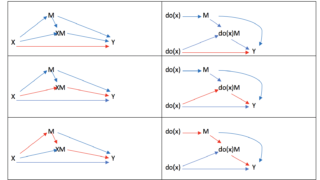
表記はpotential outcomeのフレームワークで行ってきましたが、これでは現実世界で計算をすることができません。
そこで、今回は、実際に治療(X)、媒介因子(M)、アウトカム(Y)を使用して、どのように計算していくか、empirical analogueで解説していきましょう。
おすすめ書籍↓↓
(2025/03/31 15:46:32時点 Amazon調べ-詳細)
Causal Mediation AnalysisのEmpirical Analogue
Causal Mediation Analysisをする場合ですが、大きく分けて
- Outcome regression
- G-method
の2パターンがあります。
今回は、まずg-methodの1つであるg-computation (g-formula またはstandardization)のフレームワークで考えていきましょう。
もちろんIPWでも、sequential g-estimationでも導き出すことができます。
Total Effectのg-formula
まず、total effectのg-formulaを記載してみましょう。
- Total Effect = E(Yx) – E(Yx*)
でした。まずE(Yx)の部分にg-formulaを使ってみると、以下のようにempirical analogueが作れます。Cで全てのbackdoor-pathを閉じることができると仮定をすると
- E(Yx)
- = ΣcE(Yx, c) *Law of probability
- = ΣcE(Yx|c) P(c) *Law of probability
- = ΣcE(Yx|x, c) P(c) *Conditional exchangeability
- = ΣcE(Y|x, c) P(c) *Consistency
となります。ここまで持ち込めれば、potential outcome がempirical analogueになりました。これは因果推論(Causal Inference)の基本中の基本です。
例えば、Total Effectをg-formulaで記載すると、
- Total Effect
- = E(Yx) – E(Yx*)
- = ΣcE(Y|x, c) P(c) – = ΣcE(Y|x*, c) P(c)
となります。
これがg-formulaにおけるmarginal causal effectです。
さらに、ここからmediator (M)を使用して、Yx= YxMxにします。
- E(Yx)
- = ΣcE(Y|x, c) P(c)
- = ΣmΣcE(Y, m|x, c) P(c) *Law of probability
- = ΣmΣcE(Y|x, m, c)P(m|x, c) P(c) *Law of probability
- = E(YxMx)
となります。
ここから、
- E(YxMx) = ΣmΣcE(Y|x, m, c)P(m|x, c) P(c)
となりますが、赤色で記した箇所がYとXの直接の関係、青色で記した箇所がXがMを介しYに与える箇所と言えます。
つまり、
- Y model = E(Y|x, m, c)
- M model = P(m|x, c)
の2つがΣ(summation)を介して繋がっているとも言えます。
4つのnested counterfactualとg-formulaについて
ここで4つのnested counterfactualとg-formulaを整理してみましょう。
4つのnested counterfectualは、YxMxとYxMx*とYx*MxとYx*Mx*でした。これをempirical analogueに変更すると、以下のようになります。
- E(YxMx) = ΣmΣcE(Y|x, m, c)P(m|x, c) P(c)
- E(YxMx*) = ΣmΣcE(Y|x, m, c)P(m|x*, c) P(c)
- E(Yx*Mx) = ΣmΣcE(Y|x*, m, c)P(m|x, c) P(c)
- E(Yx*Mx*) = ΣmΣcE(Y|x*, m, c)P(m|x*, c) P(c)
となります。
Pure Natural Indirect Effectの場合
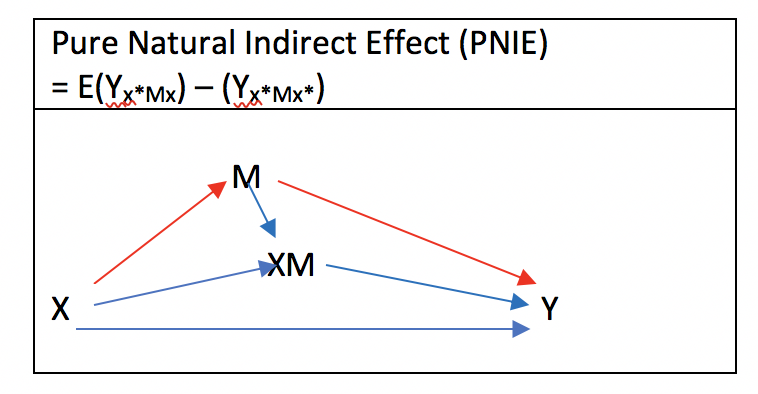
Pure Natural Indirect Effectの場合、
- E(Yx*Mx) -E(Yx*Mx*)
で記すことができます。
この場合、g-formulaを使うと、
- E(Yx*Mx) -E(Yx*Mx*)
- = ΣmΣcE(Y|x*, m, c)P(m|x, c) P(c) – ΣmΣcE(Y|x*, m, c)P(m|x*, c) P(c)
となります。
Total Natural Indirect effectの場合
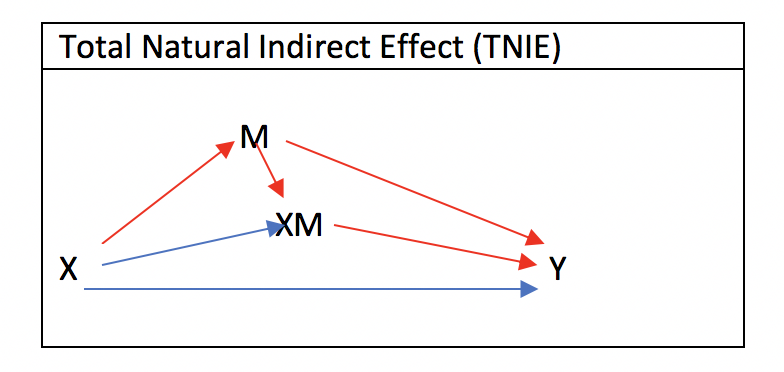
Total Natural Indirect Effectの場合、
- E(YxMx) -E(YxMx*)
で記すことができます。
この場合、g-formulaを使うと、
- E(YxMx) -E(YxMx*)
- = ΣmΣcE(Y|x, m, c)P(m|x, c) P(c) – ΣmΣcE(Y|x, m, c)P(m|x*, c) P(c)
となります。
Pure Natural Direct EffectやTotal Direct Effectの場合
こちらも同様でして、Pure Natural Direct Effectは
- E(YxMx*) -E(Yx*Mx*)
- = ΣmΣcE(Y|x, m, c)P(m|x*, c) P(c) – ΣmΣcE(Y|x*, m, c)P(m|x*, c) P(c)
Total Natural Direct Effectは
- E(YxMx) -E(Yx*Mx)
- = ΣmΣcE(Y|x, m, c)P(m|x, c) P(c) – ΣmΣcE(Y|x*, m, c)P(m|x, c) P(c)
となります。
Regression based approachの場合
次にregressionを使用した場合をみてみましょう。
Regressionはg-formulaと異なりmarginal effectは見れません。このため、conditional effectを推定することになります。
例えば、Cがbackdoor-pathを閉じるのに十分であれば、E(Yx|c)は
- E(Yx|c)
- = E(Yx|x, c) *conditional independence
- = E(Y|x, c) *consistency
- = ΣmE(Y, m|x, c) *Law of probability
- = ΣmE(Y|x, m, c)P(m|x, c) *Law of probability
- = E(YxMx|c)
となります。
g-formulaとregressionでは異なるフレームワークであるのが理解いただけると思います。
例えば、Y-modelとM-modelを
- P(M|x, c) = β0+βxx + βcc
- E(Y|x, m, c) = θ0+θxx+θmm + θxmxm+θcc
と定義すると、
E(YxMx|c)は以下のようになります。
E(YxMx|c)
= ΣmE(Y|x, m, c)P(m|x, c)
= θ0+θxx+θm(P(M|x, c) )+ θxmx(P(M|x, c))+ θcc
一方で、E(YxMx*|c)は、
E(YxMx*|c)
= ΣmE(Y|x, m, c)P(m|x*, c)
= θ0+θxx+θm(P(M|x*, c) )+ θxmx(P(M|x*, c))+ θcc
となります。
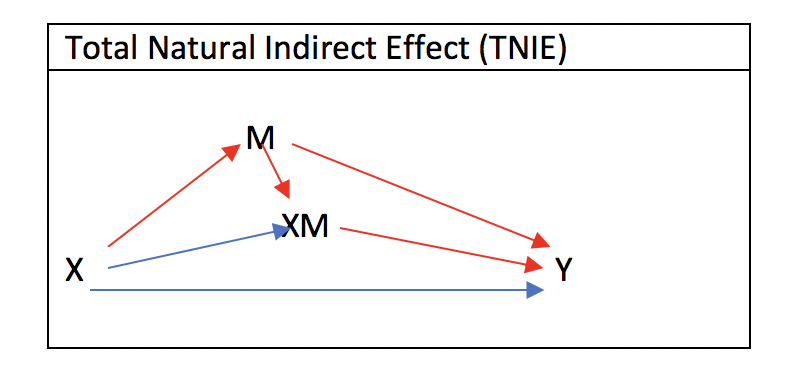
このため、TNIEは、
E(YxMx|c) – E(YxMx*|c)
= θm(P(M|x, c) – P(M|x*, c)) + θxmx(P(M|x, c)– P(M|x*, c))
=(θm+ θxmx)(P(M|x, c) – P(M|x*, c))
= (θm+ θxmx)βx(x – x*)
となります。
今回はこれまでに解説してきたCausal Mediation Analysisを、g-formulaやregressionで求める方法を解説してきました。
実際に統計ソフトを使用した解析方法については、またの機会にお伝えできればと思います。
次回はmediatorが2つある場合のcausal mediation analysisについて解説しようと思います。
おすすめ書籍↓↓
(2025/03/31 15:46:32時点 Amazon調べ-詳細)