最近はビッグデータやAIなどの普及から、データ分析に関する知識に触れる機会が非常に多くなりました。
よく耳にする言葉として、
- 因果関係 (Causation)
- (偽りの)相関関係(Spurious association)
- 交絡(Confounding)
- 選択バイアス(Selection bias)
- 逆の因果(Reverse causation)
など、様々な用語が飛び交います。
臨床医の集まる学会や、医師同士のカンファレンスなどでも飛び交う言葉ですが、実は正しく使用されていないケースも多々あります。
また、時に
- 「それって因果なの?相関なの?」
など、最もらしく発言されたはいいものの、(偽りの)相関と因果の違いをよく理解できていないこともあります。
そこで、今回はこれらの見分け方について解説していこうと思います。
結論から言うと、DAG(Directed Acyclic Graph)を使って構造的にアプローチをすれば、理解しやすいと思います。
本記事の内容
- DAGを使って、因果・相関・交絡・選択バイアスを表現する
- 因果関係
- (偽りの)相関関係(交絡)
- 逆の因果関係
- 選択バイアス
今回はModern Epidemiologyと、こちらの論文を参考に記載しています。
https://www.ncbi.nlm.nih.gov/pubmed/15308962
こちらの論文は、2004年にMiguel Hernan教授らが出版したもので、非常に多く引用されている有名な論文です。
疫学の領域では、この論文はmust readでして、ほとんどの疫学者が読んでいると思います。
DAGを使って、因果とバイアスを検討する
私は観察研究をする際にはPECO/PICOは使わず、DAGを使って研究の構造を理解するようにしています。
PECO/PICOはRCTであれば使用してもらっても構わないとは思うのですが、物事を単純化しすぎて、臨床研究で大事なバイアスの検討が不十分になってしまうリスクがあるため、私は全く使用していません。
DAGはDirected Acyclic Graphの略でして、日本語で言い換えると「有向非巡回グラフ」といったところでしょうか。
一見すると難しそうな言葉ですが、ベクトルのようなものと理解していただければ良いと思います。
DAGで因果・相関・交絡・逆の因果・選択バイアスを描いてみる
DAGを使えば、
- 因果関係
- (偽りの)相関関係(交絡)
- 逆の因果関係
- 選択バイアス
といった疫学の専門用語も簡単に理解できます。
「AがYに与える影響」を検討するとして、矢印がどこからどこに延びているのか注目してもらうのが良いでしょう。
因果関係について
 因果関係とは、とある原因(A)から結果(Y)に矢印がのびている状態をいいます。
因果関係とは、とある原因(A)から結果(Y)に矢印がのびている状態をいいます。
もう少し平たく言うと、
- ある治療(A)をすると、病気が悪化しない(Y)
- 喫煙を続けると(A)、肺癌のリスクが上昇する(Y)
このような状態をいいます。
単なる矢印ですが、いくつか重要な情報を教えてくれていて、例えば喫煙を例にすると
- 喫煙をやめれば、肺癌のリスク上昇は止まる/改善する
- 喫煙は肺癌の発症より前に起こっている
という2点です。
前者は「因果」ですので、「治療をすると回復が期待できる」「危険因子を取り除けば、リスクを下げられる」など、直接の効果を期待できます。
後者は「時間制(Temporality)」をみており、どちらが先で、どちらが後かは非常に重要です。因果をいうには、治療や危険因子が、結果より先にいなければなりません。
交絡について
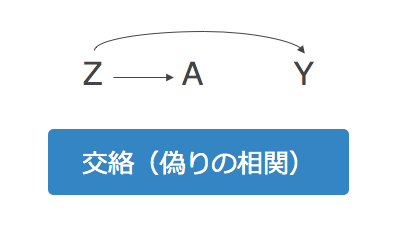
交絡のDAGは上のようになります。
- (AからYへの)直接の矢印はないが
- 原因(A)と結果(Y)の共通の原因(a common cause)がある
状態をいいます。どのような例が考えられるでしょうか?
「A = ライターの所有」、「Z = 喫煙」、「Y = 肺癌」を考えてみましょう。
喫煙者はライターを所有しています。また、喫煙者は肺癌のリスクが上昇します。この2点は疑いようがないでしょう。
しかし、とある研究者が「喫煙者(Z)」を評価せず、「ライターの所有(A)」と「肺癌(Y)」を調査してしまうと、「ライターは肺癌の原因である」と結論を下してしまいます。
しかしこの結論は間違っています。なぜなら、喫煙 (Z)が肺癌 (Y)の直接の原因だからです。
『偽りであっても、ライターは肺がんと関連しているのに、どうしていけないのだろうか?』
と疑問に思われた方がいるかもしれません。
疫学研究では「危険因子を特定して、そこに介入をして疾病を予防する」ことを目的にしています。
ライターと肺癌を例にすると、ライターの販売を禁止しても、おそらく喫煙者は別の手段(マッチなど)で喫煙を続けるでしょう。
偽りの相関は、時に間違った介入に結びつくため、慎重に評価をする必要があります。
逆の因果について

逆の因果は、原因と結果が逆転してしまった状態です。
例えば、頭部CT検査による被曝(A)が脳腫瘍のリスク(Y)を上昇させるか調査したとします。
しかし、実は脳腫瘍のある人(Y)は(画像検査でわからないくらい小さな腫瘍の時から)頭痛のためCT検査(A)をしている場合があります。
この場合、「CTが脳腫瘍を引き起こした」というより、「脳腫瘍の前兆として頭痛のある人がCT検査に来ていた」というのが正しいでしょう。
このような状態を逆の因果と言います。
近年、この逆の因果を交絡の一種と考えられています。もう一度、こちらのDAGをみてみましょう。
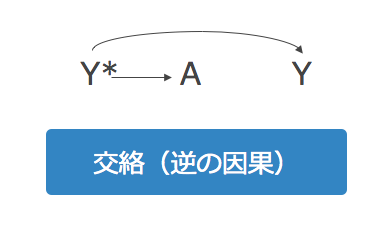
「Y*=脳腫瘍(CTで分からないくらい小さな)」
「A = CT検査」
「Y = 脳腫瘍(MRIでわかるレベルの)」
と考えると、逆の因果は実は交絡であることが分かりやすいでしょう。
CTでは分からないくらい小さな脳腫瘍のある方(Y*)が、頭痛のためCTで精査をしました。しかし、CTでは分からず、後日、MRIで検査をしたところ、脳腫瘍(Y)が発見されました。
というストーリーが考えられます。
この場合、「診断できなかった脳腫瘍(Y*)」による交絡ともいえます。
選択バイアスについて
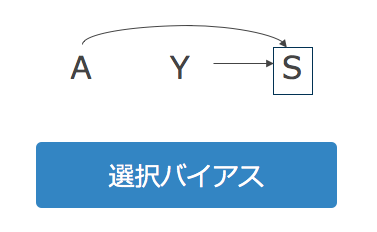
最後に選択バイアスを説明します。
選択バイアスとは、原因(A)とアウトカム(Y)の共通の結果(S)を選択した場合に生じる(a common consequence)ともいえます。
少し分かりづらいと思うので、簡単な例を考えてみましょう。
「A = 走るスピード」「Y = 身長」とします。
今回の例では、「A = 走るスピード」と「Y = 身長」に直接の関係はなかったとします。つまり、背が低くても、背が高くても、足の速い人は同じだけいる状態です。
これを「NBAの選手(S = 1)」のみで限定をしてしまうと、選択バイアスが生じます。なぜなら、
- 長身の選手は、足がそこまで早くなくても生き残れる
- 背の低い選手は、俊足でないと、NBAでは生き残れない
という2つの現象が生じてしまいます。
NBAの選手に限定して身長と足の速さを調査をしてしまうと、本来は関係のな買った「身長」と「足の速さ」が、あたかも関連しているように見えてしまいます。
このことを選択バイアスと言います。

「実際の研究では何が問題でしょうか?」
と疑問に思われたかもしれません。
疫学研究では常に選択バイアスに対する注意は必要ですが、特にケース・コントロール研究で起こりやすい傾向にあります。
近年はあまり使用されなくなりましたが、病院内のみのデータでケース・コントロール研究をすると、ほぼ間違いなく選択バイアスが入り込んできます。
なぜなら、病院内という限られたデータしか使用しておらず、一般の集団を代表していない可能性があるからです。
ここは私見になりますが、おそらく下記の研究は、選択バイアスの影響を非常に大きく受けた研究と考えています。
まとめ
今回は、DAGを使って
- 因果関係
- (偽りの)相関関係(交絡)
- 逆の因果関係
- 選択バイアス
を説明してきました。
言葉として記憶するより、構造を頭で理解していたほうが、実際に論文を読む時や、研究をするときに大きく役に立つと思います。
今日紹介した論文は、選択バイアスについて詳しく記載されていますので、またの機会にさらに詳しくご紹介できればと思います。