前回はスイスで行われたトイレ・トレーニングの観察研究のデータを解説してきました。
- 排便のコントロール
- 日中の排尿コントロール
- 夜間の排尿コントロール
- 排便・排尿すべてのコントロール
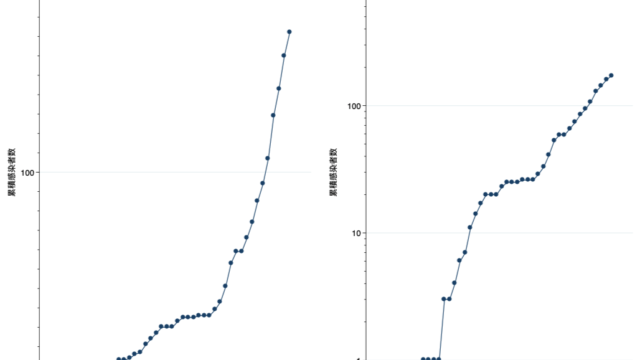
の4つにわけてグラフで示すと、以下のようになります。
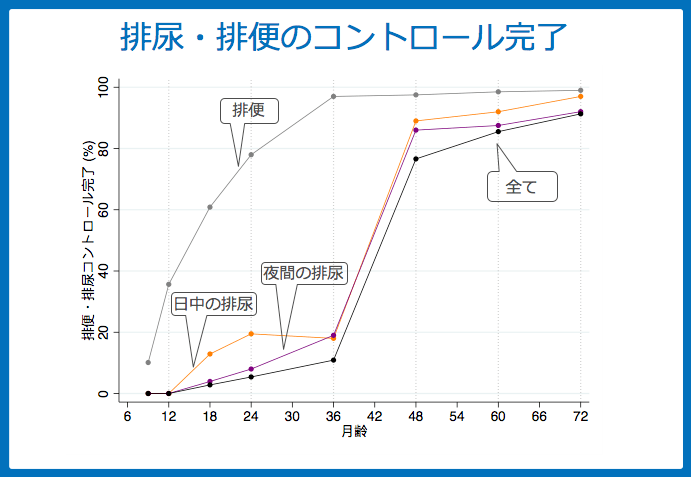
データの問題点
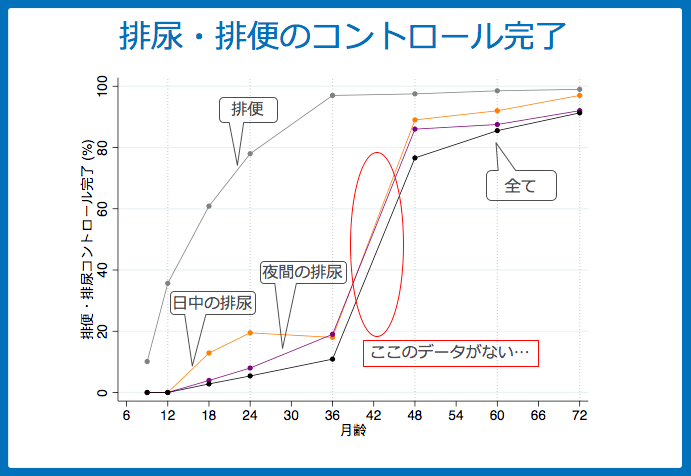
このデータの問題点がいくつかあります。
特に排尿に関して、3〜4歳にかけて劇的に変わるのは図を見れば明らかなのですが、3歳と4歳の間のデータがありません。
このため、日中と夜間の排尿がまるで同時に出来てしまっているように見えてしまうのです。
でも実際には日中の排尿がコントロールできて、しばらくしてから夜間の尿がコントロールできるようになるわけです。
今回は統計モデルを使用して、もう少し滑らかな曲線を描いてみようと思います。
統計モデルを組み立ててみる
以下は統計学的な話(ややマニアック!?)になりますので、面倒でしたら飛ばして下の最後の図を楽しんでください。
今回はY軸に確率、X軸に時間があります。
この場合、確率(a/N)を扱う統計モデルを使用するか、あるいはaを数として扱うモデルを使用するかのいずれかになります。
代表的なモデルを列挙すると
- Logit
- Probit
- Poisson (or Negative binomial model)
あたりが使い易いと思います。
細かい前提の話は抜きにして、簡単に統計モデルの解説をしていきます。
Logit について
Logitはロジスティック回帰分析のことで、log (odds)を使います。
確率をpとすると、
- odds = p / (1 – p)
となり、さらにoddsにlogを使えば、log (odds)となります。
このlog (odds)のことをlogitといいます。
今回は
- logit (p) = a + b1 x Time + b2 x log (Time)
という数式を用いています。
Log (time)を入れたのは、時間が進めば、ある一定の数値(P)に収束すると予測 できるためです。
ProbitとPoisson(ポワソン)について
もちろん、Probitでも同じようにモデルを組むことは可能です。
Probit regressionを使用する場合、確率をz-scoreに変換する必要が出てくるため、統計結果の解釈がlogitと比べて、やや分かりづらくなることがあります。(Logitも十分、わかりづらいとは思いますが…)
Logistic regressionよりも、両隅の数値(今回でいうと9ヶ月や70ヶ月あたり)が正確になりやすいという利点もあります。
Poisson(ポワソン)regressionを使用する場合は、確率はそのまま使えず、例えば
- log(a) = α + β1 x Time + log (N)
となります。aは完了した人数、Nはその集団全員の数を入れて解析することになります。
この場合、「Log(N)」のことをoffset (オフセット)と呼んでいます。
統計モデルを組んだ結果
Logitモデルで統計モデルを組んだ結果、以下のような図になります。
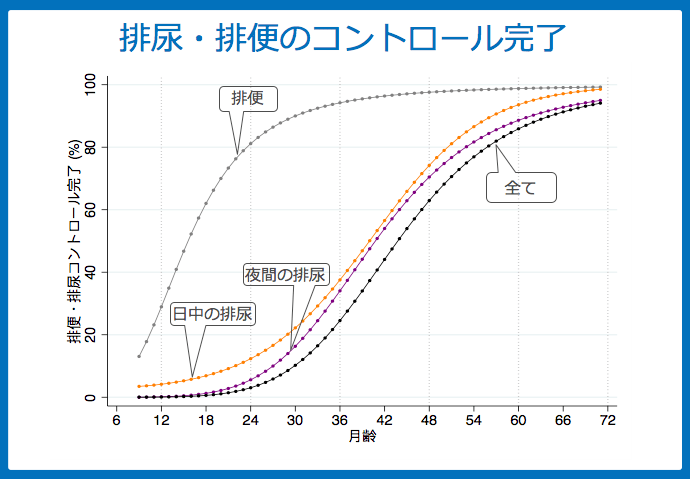
だいぶスムーズなグラフになりました。
あくまでグラフからの予測値になりますが、日中の排尿がコントロールできるようになってから(オレンジ)、排便・排尿の全てが完了するまで(黒)は平均して6ヶ月程度のインターバルがあるように見えます。
(実際には、もう少し時間がかかることもあると思いますが…。最初のグラフより随分マシになったので、ご容赦ください)
データのポイントが少ないため、あくまでも予測値になりますので、ご了承ください。
続きはこちら↓↓