前回まで、メタ解析の考え方、手法などを説明してきました。

こちらの論文を用いて、メタ解析を実際に行ってきました。
前々回は、固定効果とランダム効果、Mantel-Haenzel法とInverse-variance法を用いて、実際にメタ解析を行いました。
そして、前回は異質性が非常に高く、第3の因子(Effect modifier)が治療効果を修飾している場合の評価の仕方について解説してきました。
今回は、
- 出版バイアスの評価
- アウトカムが連続変数の場合
を実践を交えながら、解説していこうと思います。
出版バイアスの評価をする
以前、2回に分けて出版バイアスの評価方法について解説してきました。
こちらの2記事では、
- Funnel Plotによる視覚的な評価方法
- Egger’s test
- Begg’s test
の三通りを説明しています。
今回は、これら3つを実際にデータを使いながらみていきましょう。
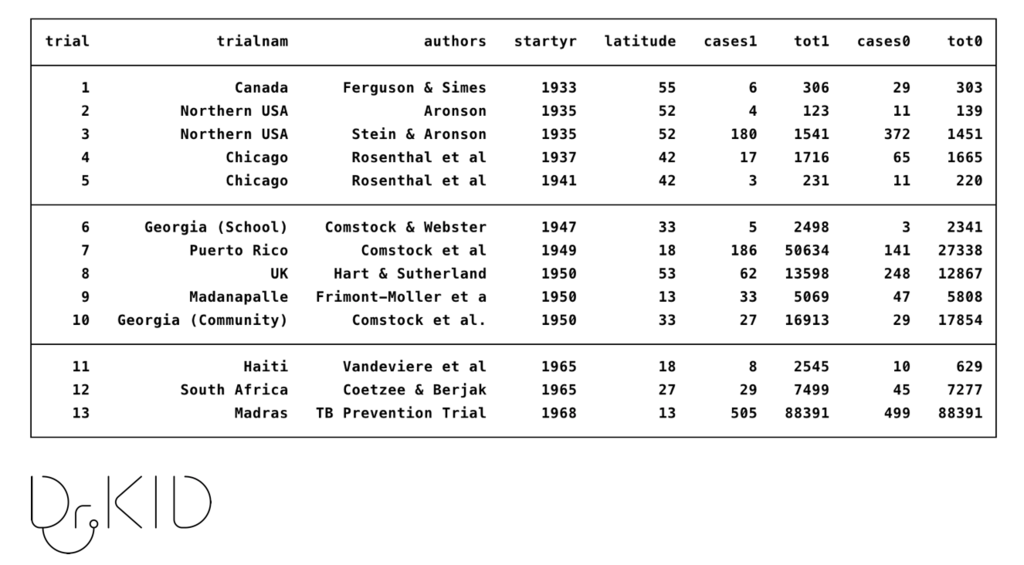
データはいつも通り、こちらの解析結果を使います。
Begg’s test
まずはBegg’s testについてみていきましょう。
- metabias
というコマンドを使用すれば検定できます。
Begg’s testは、ケンドール(Kendall)の順位相関という指標を使った、non-parametric testでした。
こちらがstataのoutputになります。

Egger’s test
次にEgger’s testをしてみましょう。
Egger’s testは、parametric検定になります。このため、Begg’s testの結果より検定力は大きい傾向にあります。
解析結果とコマンドは以下です。

Egger’s testもBegg’s testも統計学的な有意差はありませんでした。
Funnel Plot
次に、Funnel plotをみてみましょう。
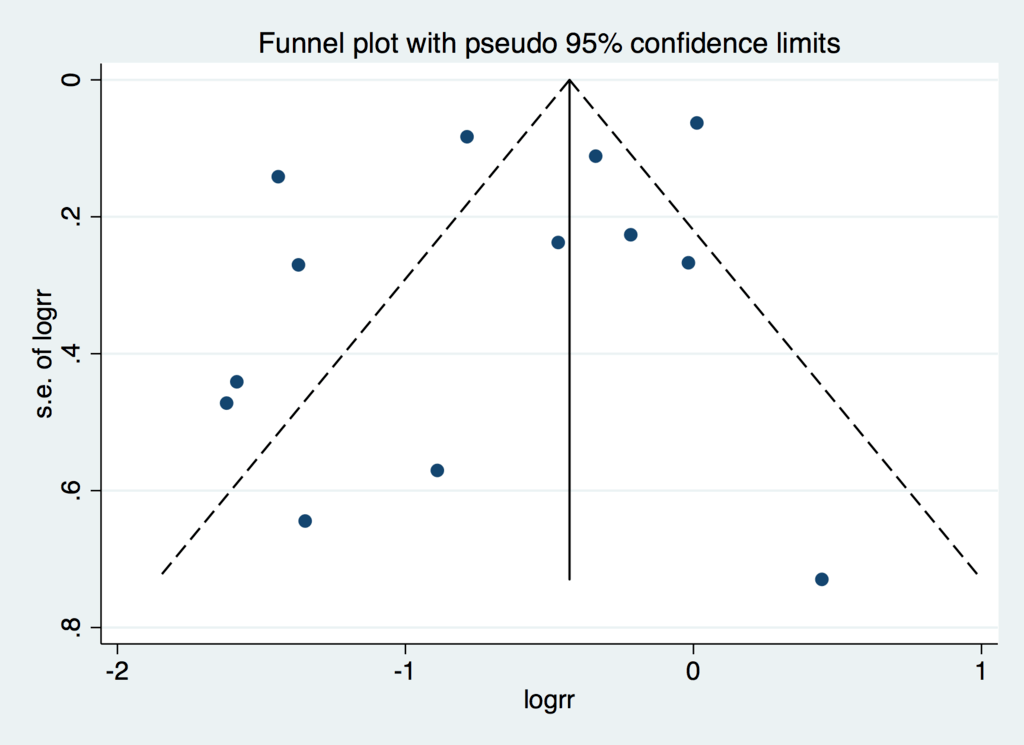
わりと左右対称ですが、点の位置(ここの研究結果)のばらつきが激しいのがみてとれます。
今回は「緯度(latitude)」による異質性を考慮してみようと思います。
まずは研究が行われた国の緯度によってワクチンの予防効果が異なるか見てみましょう。

緯度を低い順に並べてみると、
- 緯度の低い国は治療効果が低い
- 緯度の高い国は治療効果が高い
傾向にありそうに読み取れます。
サブグループで解析をする
緯度が異質性のソースになっていそうなので、緯度の低いグループと高いグループに分けて解析をしてしまえばいいのです。
ここでデータを
- 緯度が35度以上
- 緯度が35度未満
の2つのグループにわけてランダム効果を用いてみます。
緯度が35度以上
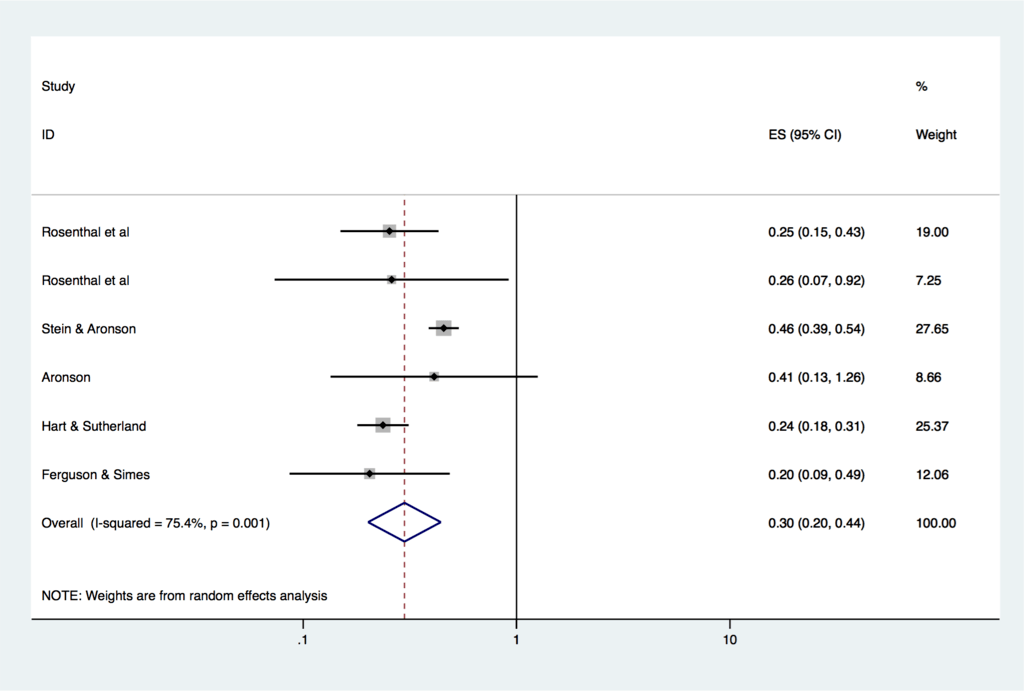
緯度が35度以上の結果はこちらになります。
予測した通り、全体での解析結果と比較して治療効果は大きく、
- RR 0.30 (95%CI, 0.20-0.44)
となっています。95%信頼区間が1を跨いでないので、統計学的な有意差があります。
緯度が35度未満
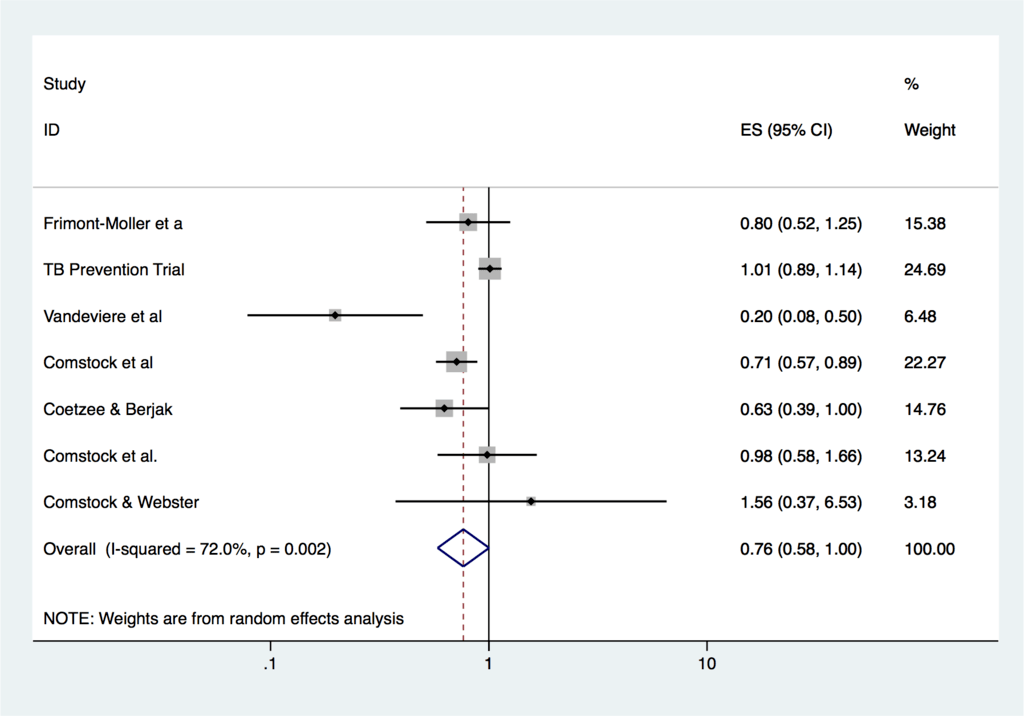
こちらが35度未満での結果となります。
治療効果は緯度の低い地域では低く、
- RR 0.76 (95%CI, 0.58-1.00)
と統計学的な有意差が消えてしまいました。
緯度の高い地域 vs 低い地域で治療効果に差があるか検討をする
- 35度以上:RR 0.30 (95%CI, 0.20-0.44)
- 35度未満:RR 0.76 (95%CI, 0.58-1.00)
と2つの結果を出しました。
この2つのグループの結果が統計学的に異なるか(異質性といえるか)を解析してみましょう。
緯度が高い地域(higherlat)のほうが、統計学的に優位に予防効果が大きいという結果でした(P = 0.002)
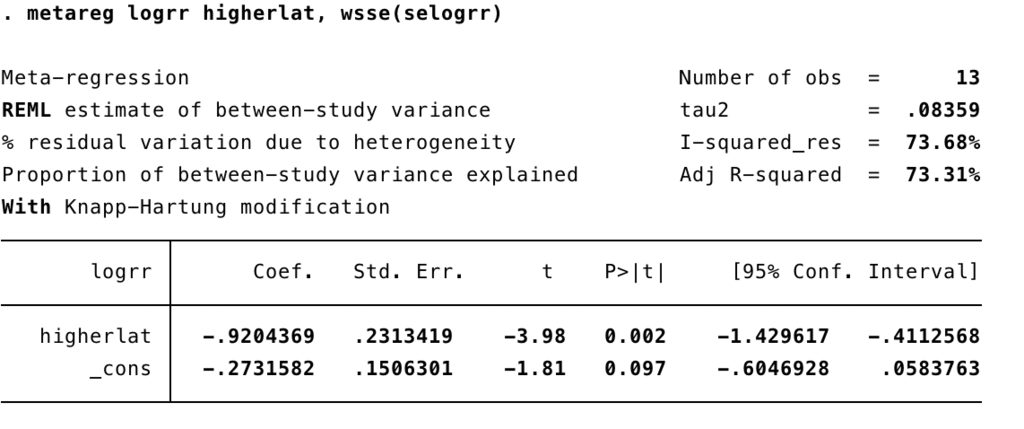
メタ回帰分析で異質性を評価する
- 低い緯度の国々のほうが衛生環境が悪いことが多い
- 年度が早いほうが、衛生環境が悪い
といったことが予測できるため、これら2つがワクチンの結核予防効果にどのように影響を与えるのか、メタ回帰分析でみてみましょう。
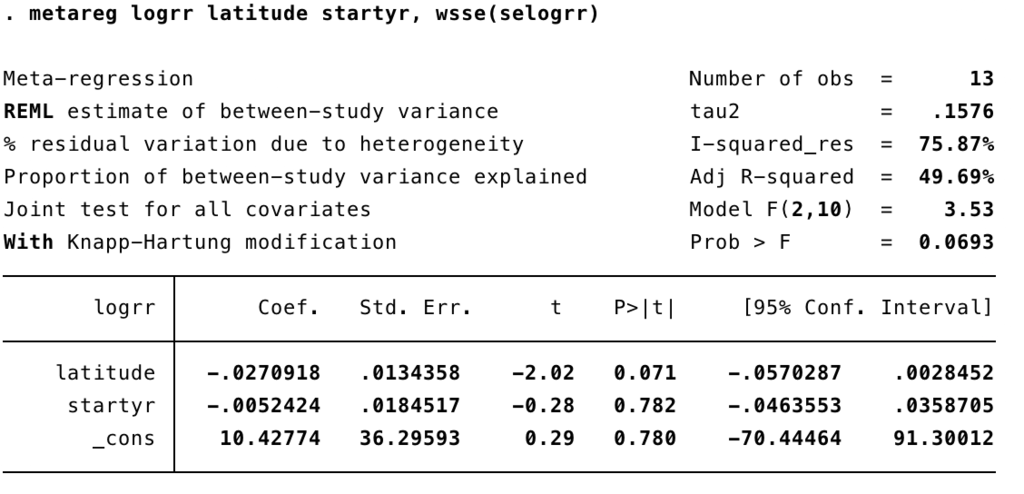
- 緯度が1度あがると、治療効果(RR)は exp(-0.027) = 0.97倍に下がる
- 研究年が1年遅れると、治療効果は exp(7.82) = 0.94倍に下がる
といえます(統計学的な有意差はありませんが)。
つまり、この結果から、
- 緯度が高いほど、予防効果が大きい
- 研究した年度が遅いほど、予防効果が大きい
といえます。
連続変数の検定について
次はこちらの研究をみてみましょう。
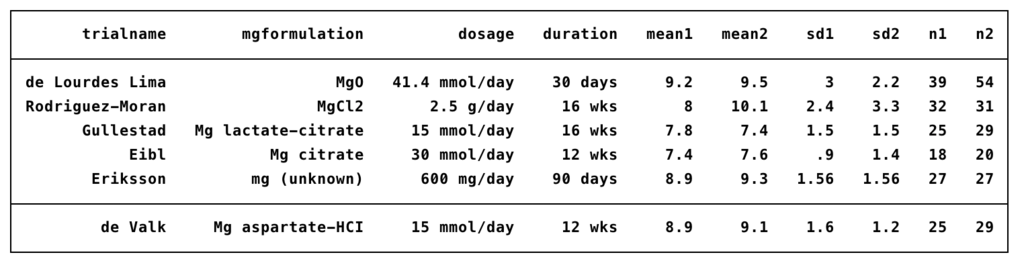
こちらのメタ解析では、マグネシウムがHbA1cに与える影響をみています。
- 重み付け平均の差(weighted means difference)
- 標準化平均の差(standardized means difference)
の2つをみてみましょう。
ここから、アウトカムがあり/なしの2択から、連続変数に変わっています。
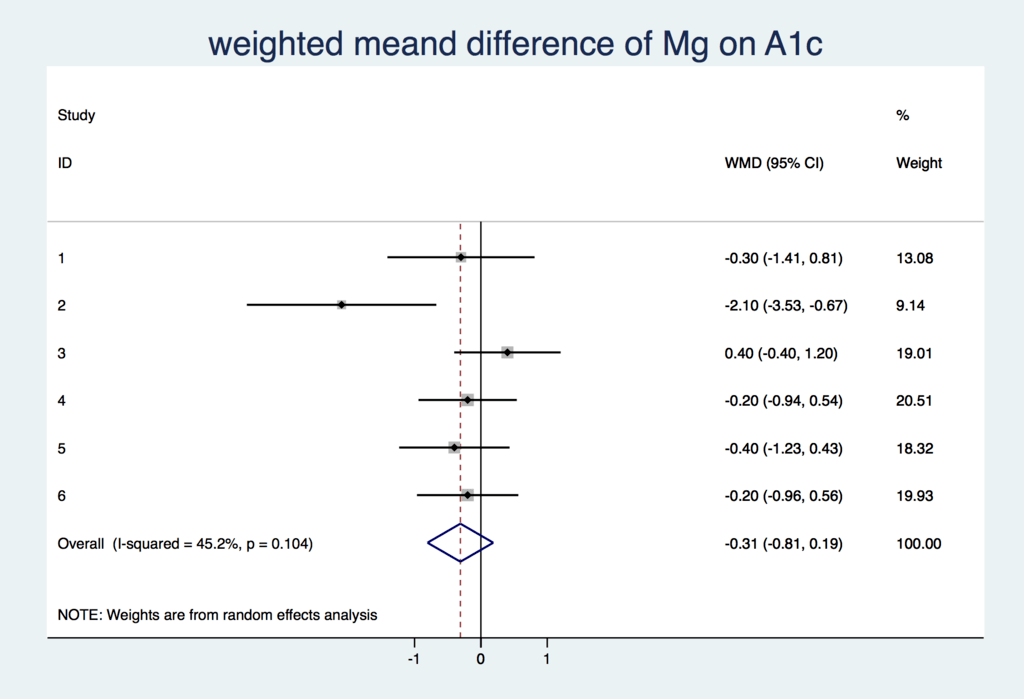
重み付け平均の差(weighted means difference)

こちらが結果になります。マグネシウム投与群と非投与群でのHbA1cの差は
- -0.309(95%CI = -0.805, 0.187)
と95%信頼区間が1を跨ぐため、統計学的な有意差はありません。
標準化平均の差(standardized means difference)
次に標準化平均の差をみてみると、以下のようになります。
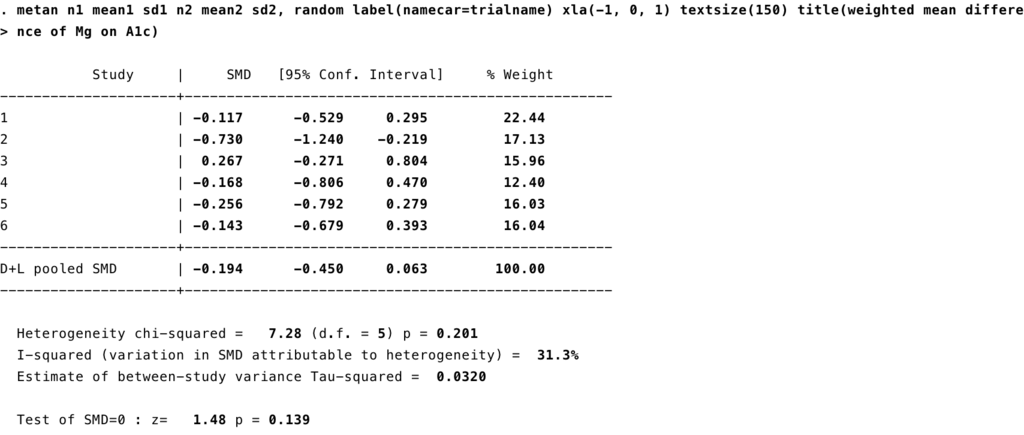
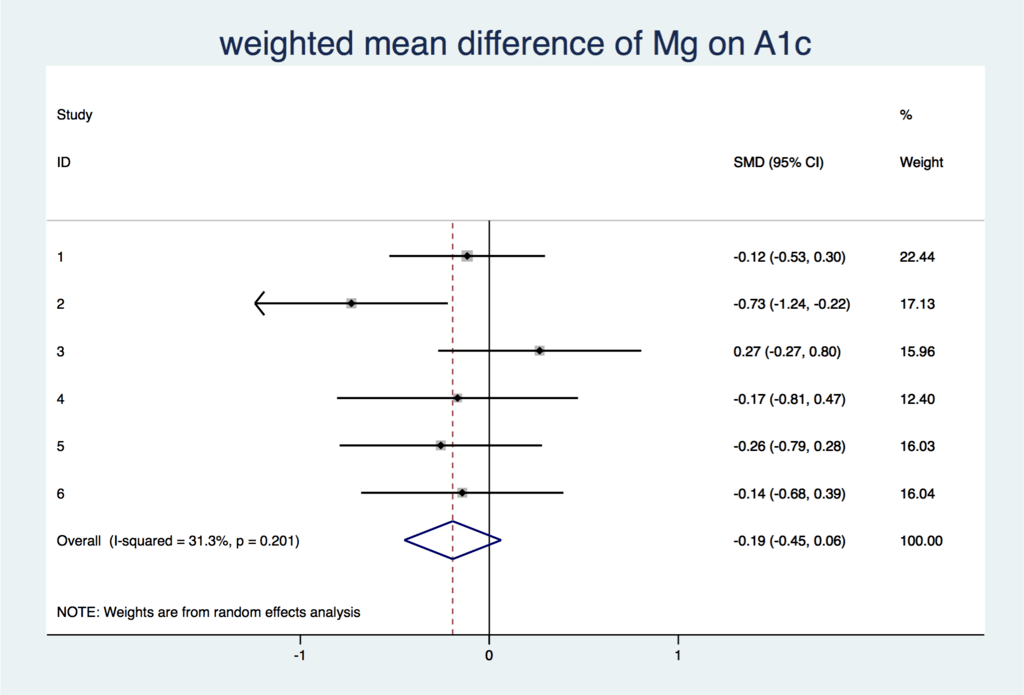
こちらも、標準化した平均の差は
-
-0.194 (95%CI, -0.679〜0.393)
となります。こちらも95%CIが1をまたいでいるので、統計学的な有意差はありません。
Forest Plotは以下の通りになります。
まとめ
今回は、Stataを使いながら、出版バイアスやアウトカムが連続変数の場合の対処について、実践を交えながら簡単に説明しました。
今回でメタ解析の解析は一旦終了にしようと思います。
おすすめ本はこちら