前回は因果関係の証明において重要な条件について簡単に説明してきました。
・時系列として、原因(治療など)が先、結果が後
・事実と反事実の両方がある
の2つが重要です。
また「因果関係」と一言でいっても、実は4つのタイプがあり、
1) Immune (免疫)
2) Causative(原因)
3) Preventive(予防)
4) Doomed (運命)
があります。
かなりラフにいうと、上の2つの条件を満たせば因果関係がわかり、この4つのタイプのどれかに落とし込むことが可能となります。
前回の説明の最後に少し言及しましたが、とある結果が起こるのに原因が1つとは限りません。原因が2つ以上重なって、ようやく結果(アウトカム)が出ることがあります。
このような場合は「Sufficient-Component Causal Model」を使ってみると、原因と結果(因果関係)の理解が深まるかもしれません。
今回は「Sufficient-Component Causal Model」について説明していきます。
1) 原因について
前回説明した「反事実モデル」と同様に、「Sufficient-Component Causal Model」も因果関係を考える上で必要なフレームワークです。
「 Sufficient-Component Causal モデルは、Modern Epidemiologyの著者であるRothmanらが中心に考案された因果推論のモデルです。
Sufficient-Component Causal Modelの解説に入る前に、「原因」について簡単に定義してしまいましょう。
「原因」とは
- 結果(アウトカム)より前に起こっている
- 結果が生じるのに必要な条件である
- この特定の「原因」がなければ、結果は生じない
(あるいは結果が生じるタイミングが異なる)
という条件といえます。
2) 実際にSufficient-Component Causal Modelをみてみよう
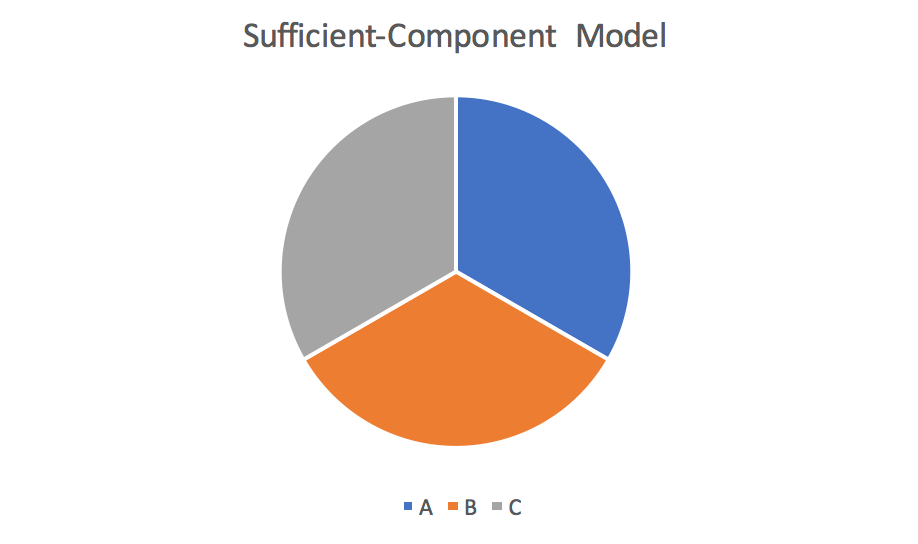
いきなりですが、「かっこつけた名前のくせに、ただのパイチャート(円グラフ)かよっ!」と突っ込みたくなる方が多数いると思います。
その通りでして、別名「Causal Pie(因果のパイ)」とも言われています。
見かけ上は円グラフですが、記述統計で使う円グラフとは考え方は少し異なります。
簡単にいうと、それぞれのパイ(pie;原因であるA, B, C)を満たしたときに、結果(円)が生じる、という意味です。
3) 因果のパイ(Causal Pie)の例
因果のパイ(Causal Pie)の例として、「雨がふり、もともと手すりのない滑りやすい階段で、転んでしまった」という事象を考えて見ましょう。
この場合;
- A = 雨が降った
- B = 階段が滑りやすい
- C = 手すりがない
という3つの条件があり、「転んだ」という結果が起きます。(他の条件は必要でなかったと仮定しましょう)
A, B, Cは上の図でいう1つずつのパイにあたります。
「転んだ」というのは1つの結果(アウトカム)ですので、円全体を表します。
この3つの条件は原因といえます。なぜなら、
- A:雨が降らなければ、転ばなかった
- B:もともと階段が滑りにくければ、転ばなかった
- C:手すりがあれば、転ばなかった
と想定されるからです。
4) Sufficient CauseとComponent Causeについて
まずはComponent Causeとは上の図でいうと、A, B, Cの1つずつをいいます。
つまり、
- A = 雨が降った
- B = 階段が滑りやすい
- C = 手すりがない
という3つは、すべてComponent Causeといえます。
別の言葉でいいかえると、結果が起こるのに必要な原因(条件)の1つ1つを「Component Cause」といえます。
一方で、Sufficient Causeは、その名の通り、結果を起こすのに十分な原因群(十分条件)といえます。
今回の転倒の例でいうと、A, B, Cの3つが揃った状態のことを「Sufficient Cause」といえます。
5) Necessary Causeについて
少しややこしいですが、Component CauseとSufficient Cause以外にも「Necessary Cause」という概念があります。
「Necessary Cause」は「必要な原因(必要条件)」ともいえます。
とある結果(アウトカムや疾病)が起こるのに、必ず必要な原因(条件)といえばわかりやすいでしょう。
6) Necessary Causeの例
Necessary Causeの例としてわかりやすいのは感染症です。
例えば、HIVに感染し、
- 適切な治療がなされなかったり
- もともと免疫不全症があったり
- 治療のコンプライアンスが悪い
などがあると、エイズ(AIDS:後天性免疫症候群)を起こします。
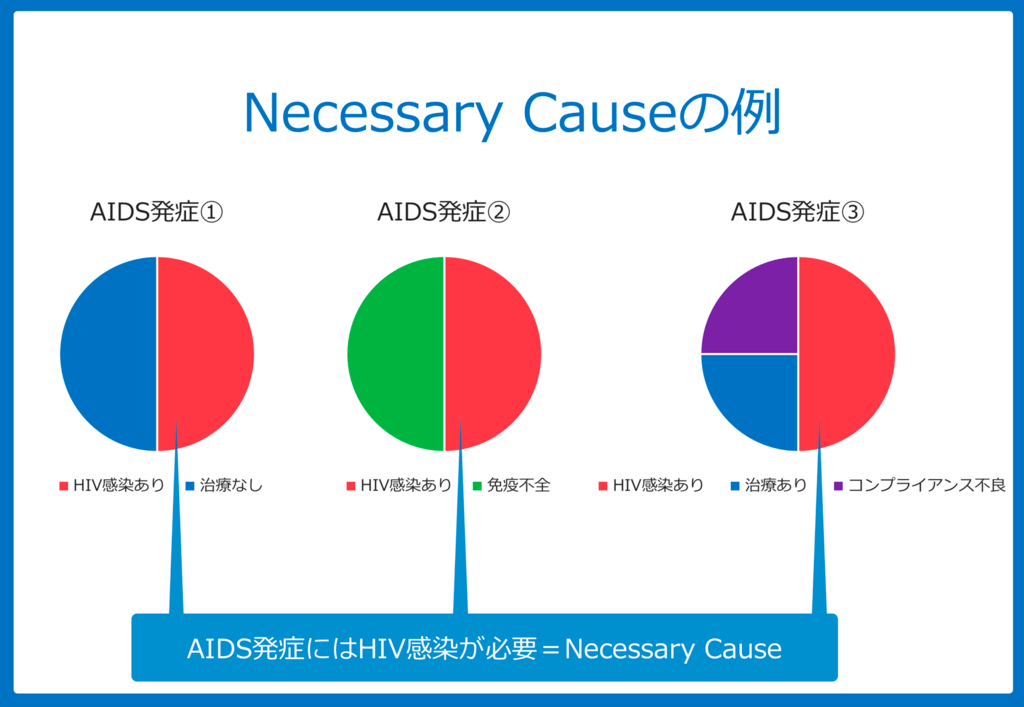
この3つのCausal Pie(因果のパイ)をみると、すべてのパイにおいてHIV感染があります。
このようなComponent cause(個々のパイ)のことを、Necessary cause(必要な原因)といいます。
よくよく考えてみると当たり前のことですが、AIDSを発症するには、HIVに感染しないと発症しようがありません。
他の例としては、リウマチ熱も溶連菌に感染したことがなければ、基本的には発症しないでしょう。
7) Sufficient-Component Causal Modelの利点と欠点
このモデルの利点は、
- 視覚的にわかりやすい
- アウトカムに必要な因子の組み合わせが分かる
といった点があげられます。
その一方で、欠点としては、
- 原因の時系列がわからない
- 原因を2つ(あり/なし)に分ける必要がある
(タバコ10本/日以上vs 以下など) - 組み合わせ次第で、パイの数は無限になる
というのが欠点になります。
まとめ
今回はSufficient-Component Causal Modelについて簡単に解説してきました。
視覚的に分かりやすいのが利点ですが、時系列がわからない、組み合わせ次第で無限になる、といった欠点があります。
他にも反事実モデルとあわせて、こんな考え方もあるのか、と頭の片隅にいれておくと良いでしょう(実は、私は実際の研究では、このモデルはあまり使用していません)。