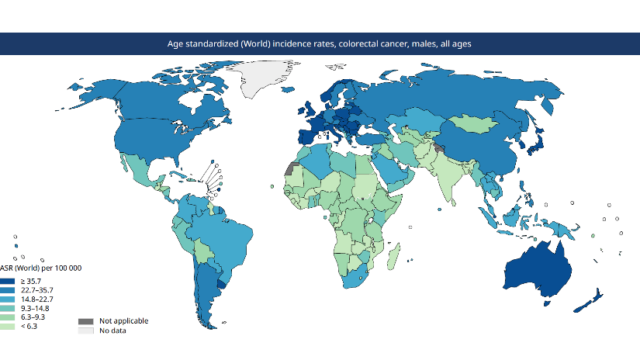
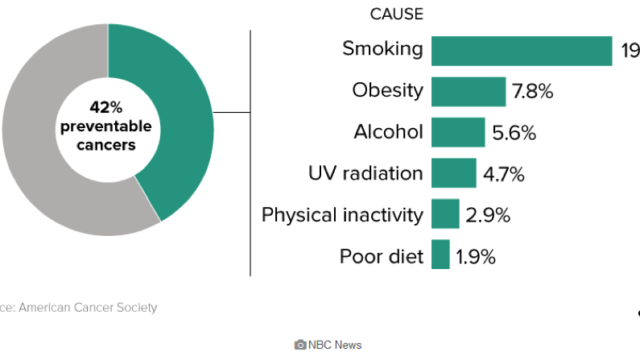
前回、感染症疫学(Infectious disease epidemiology)」の「基本のき」であるR0(基本再生産数)について解説してきました。
R0は、新規に感染症にかかった1人が、免疫をもたない集団に入った場合、感染させることができる人数のことをいいました。
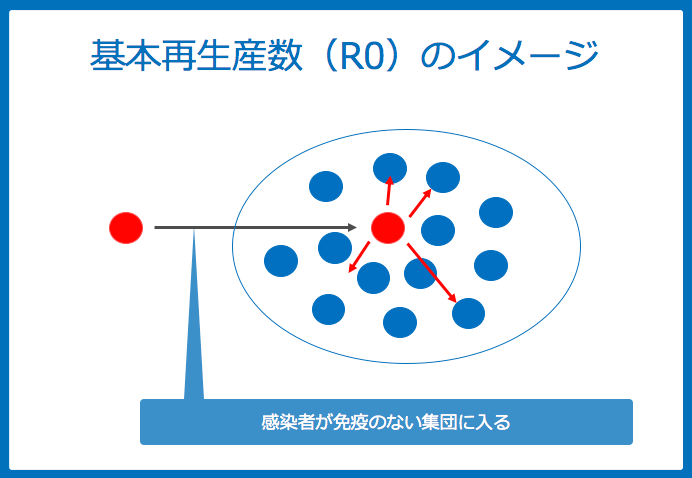
今回は R (実効再生産数)とS-I-R モデル(別名:Reed-Frost Epidemic Model)について解説していければと思います。
R(実効再生産数)について
R0は「基本再生産数」のことで、流行の初期の再生産数(感染者が何人の非感染者に疾患を移せるか?)を表す指標でした。
一方で、Rは「実効再生産数」といい、流行しだしてから(初期ではない時期に)、感染者が非感染者にどれだけ疾患を移すことができるか?、という指標になります。
R0 と R について
R0は「流行の最初の段階」であるため、研究をした集団では一定です。
一方で、非感染者の数は、流行が始まってから現象していくため、Rは計測する時間によって異なります。
R と R0 を数式で示すと
- R = R0 x 非感染者の割合
となります。(*母集団の人々がランダムに接触する場合)
流行とRについて
R < 1 になれば、感染症の流行は終わり、感染症は徐々に収束していきます。
人の出入りがない集団(Closed population)のほうが、感染症の流行は収束しやすい傾向にあります。
当たり前ですが、人の出入りがなければ、
- 感染者は軽快して、免疫を獲得し
- 非感染者の数がどんどん減っていく
からです。
S-I-R モデルについて
S-I-Rモデル(Reed-Frost epidemic model)は
- Susceptible(免疫のない人たち)
- Infected(感染した人たち)
- Recovered and Immune(感染が軽快して、免疫を獲得した人)
の頭文字(S-I-R)をとったものです。
ほとんどの感染症は、免疫のない人たち(S:susceptible)の一部が感染して(I:infected)、最後に回復して免疫を得る(R:Recover and immune)という経過をたどることに注目し、数理モデルを作りだしたのです。
人の出入りのない閉ざされた集団の場合(Closed population)
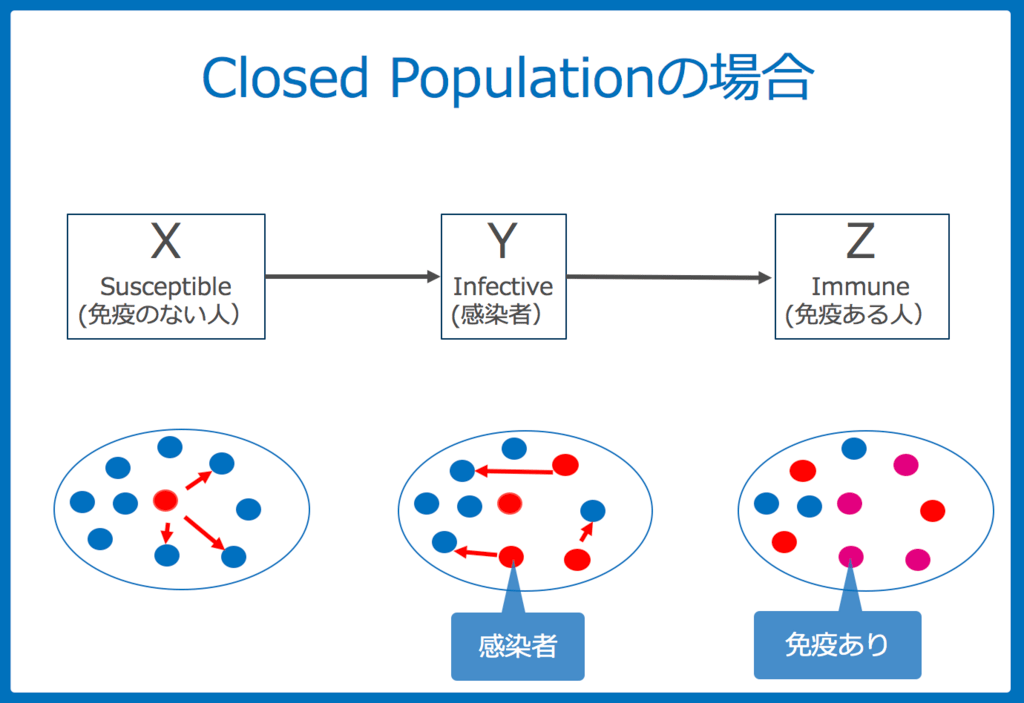
人の出入りがない閉ざされた集団(Closed Population)の場合、上の図のようになります。
時間とともに感染症は広がる一方で、免疫を獲得して回復するため、必ず感染症の流行は収束します。
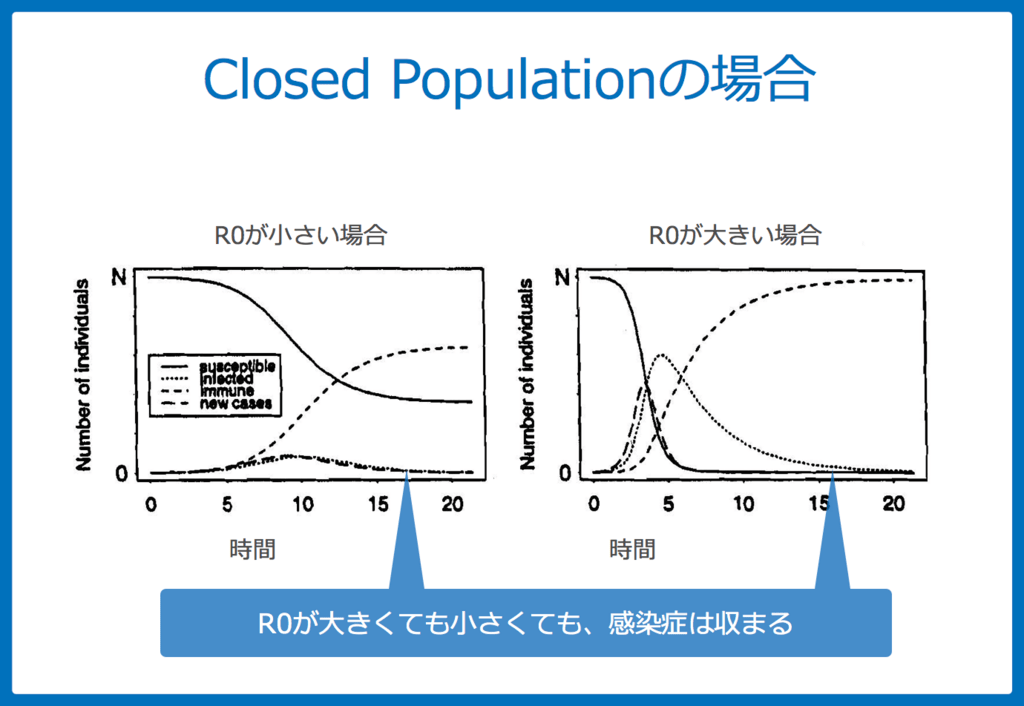
人の出入りのある集団の場合(Open population)
一方で、人の出入りが自由にある集団(Open population)の場合、感染症の流行は収まるとは限りません。
なぜなら、未感染の人が集団に入ってきますし、感染者や免疫をもった人を含め、母集団から出ていってしまう人がいるからです。
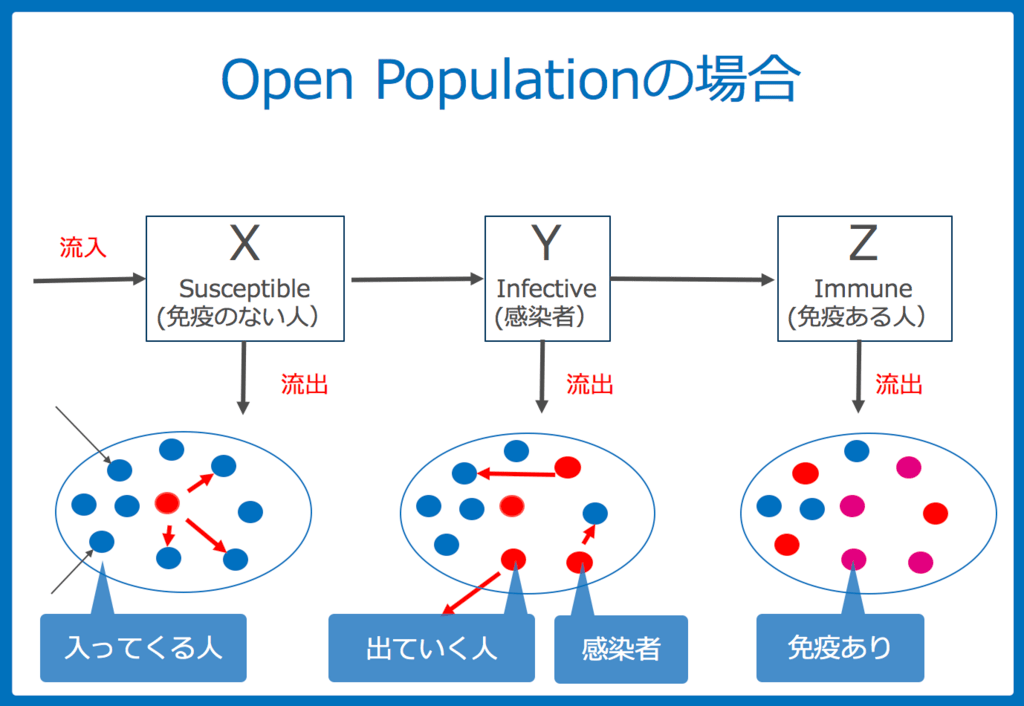
S-I-Rの人々以外に、集団に入ってくる人、集団から出ていく人を換算すると、以下の図のようになります。
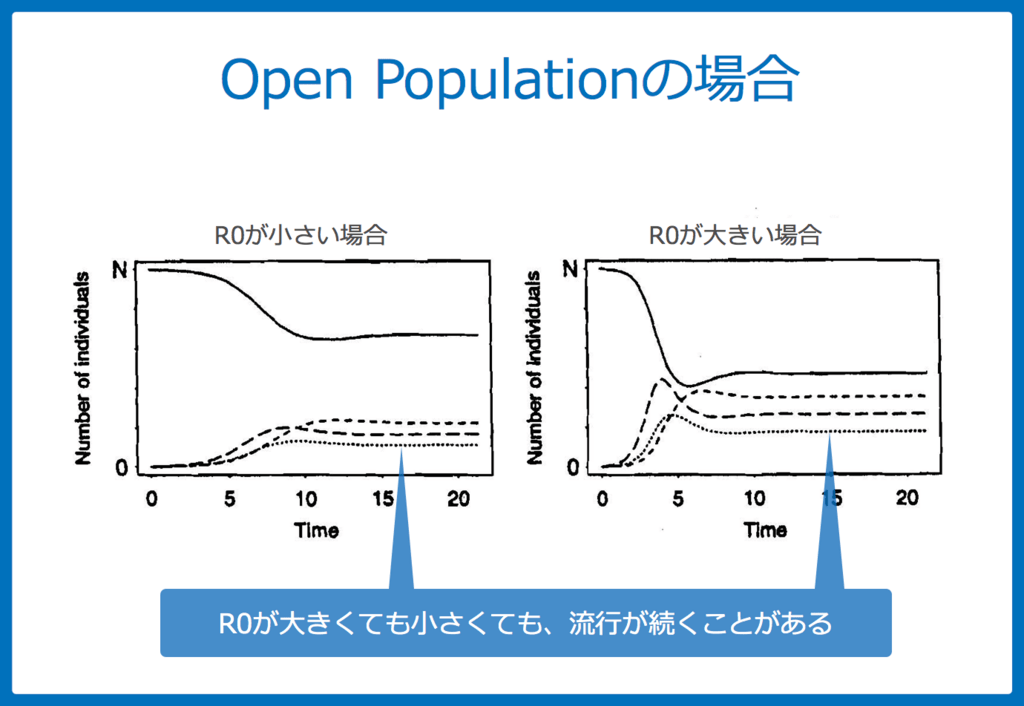
S-I-R モデルの欠点
S-I-Rモデルによって、感染症の流行を数式として理解できるようになりましたが、このモデルにも沢山の欠点があります。
例えば、人々の接触はランダムである(Random mixing)という仮定をしています。
人々の行動は、本当に「ランダム」でしょうか?と疑問が湧いてくると思います。
S-I-R モデルが不向きな状況
例えば、HIVなどの感染症は、S-I-Rモデルは適していないといわれています。
理由はいくつかあります。
例えば、特殊な人々(風俗や違法薬物使用者)のみで蔓延しやすい傾向にあります。
また、男–>女、女–>男への感染率も異なります。
この場合、random mixing(ランダムな接触)を仮定するのは難しく、別のモデル(Agent baset modelなど)が必要といわれています。
まとめ
今回は実効再生産数とSIRモデルについて解説してきました。
人の出入りのない閉ざされた集団であれば、感染症の流行は最後は収束します。
SIRモデルにも沢山の前提が置かれており、使えない状況も多数あります。
次回の土曜からはメタ解析について解説していきます。