前回、システマティック(系統的)レビューとメタ解析における、Heterogeneity(異質性)とその統計学的な評価方法について解説してきました。。
研究間でのHeterogeneity(異質性)が少なければ、そのままメタ解析を行うことができます。
メタ解析では、統計学的なモデルを作るときに
- 固定効果(Fixed effect)
- ランダム効果(Random effect)
を選びます。
今回は、この2つの違いを中心に解説していこうと思います。
メタ解析について
メタ解析(Meta-analysis)とは、統計学的な手法を用いて複数の研究結果を統合します。
統計学的な手法で「統合」するのですが、なんでもかんでも統合できるわけではありません。その前に、
- 個々の解析結果は「統合可能である」
という前提を満たさなければなりません。
メタ解析を行う理由
復習になりますが、メタ解析を行う理由は;
- Type II error(偽陰性)を減らす
- 研究結果の generalizability(外的妥当性)を広げる
- 異質性の原因を探索する
などがあげられます。
固定効果とランダム効果
メタ解析では固定効果(Fixed effects)とランダム効果(Random effects)のいずれかを使用します。
結論から先にいいますが、基本的にはランダム効果(Random effects)の使用をお勧めします。というのも、固定効果を使える状況はかなり限られているためです。
固定効果に用いられる前提について
固定効果(Fixed effect)では、
- 全ての研究は同じ効果量(effect size:想定される治療効果の大きさ)である
- 研究間での結果のバラツキはサンプリングエラーで全て説明ができる
という2つの前提を用いています。
固定効果はやや無理な前提
まず「Effect sizeが等しい」という前提についてです。
例えば日本、米国、中国、ヨーロッパ、東南アジア、アフリカで行われた研究をメタ解析するとして、
- 全ての国で行われた研究で同じ治療効果を認める
という前提をfixed effect(固定効果)では認めています。
やや無理な前提であることが理解できると思います。
ひょっとしたら治療効果には人種差があるかもしれないですし、それぞれの居住環境でも治療効果に違いがでることはよくあります。
固定効果は「研究間での違い(between study error)」を無視しているともいえます。
ランダム効果(Random effect)とは
固定効果(Fixed effect)では、やや無理な前提が必要になりますが、ランダム効果(Random effect)ではもう少しゆるい前提になります。
ランダム効果では効果量(effect size)が研究間で異なることを許容してくれます。
ランダム効果では、研究間でのばらつきを許容しながら、全ての研究に共通する治療効果を探索することになります。
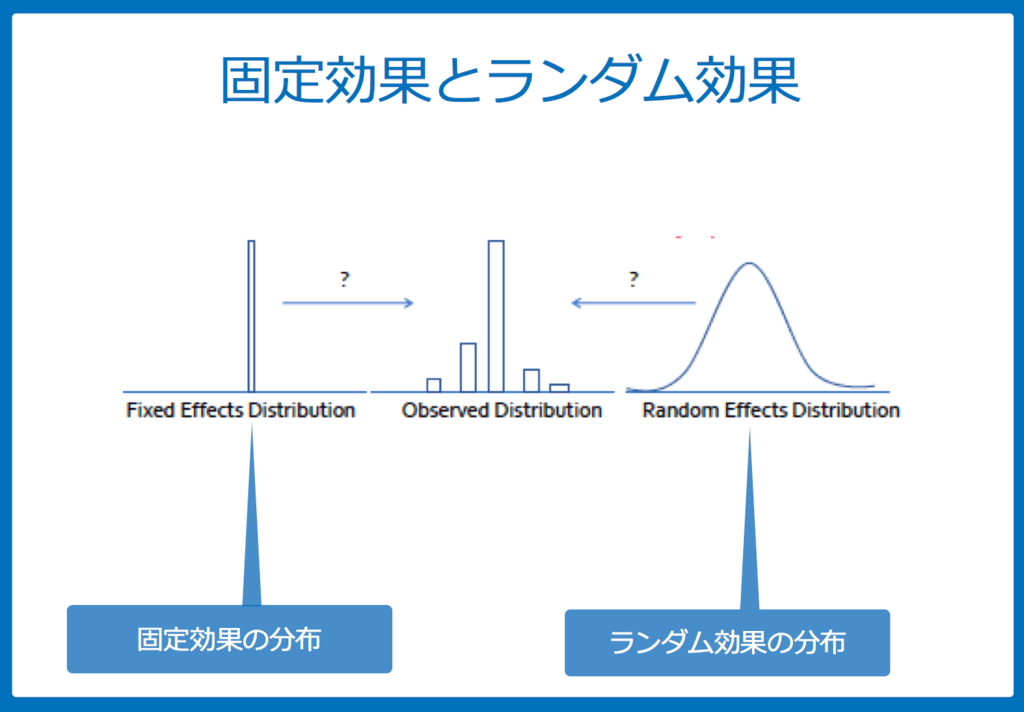
分散からみた固定効果とランダム効果
もちろん全てに当てはまるわけではありませんが、ランダム効果のほうが保守的(conservative)な結果となるケースが多いです。
これは、それぞれの分散をみれば明らかです;
- 固定効果:研究内での分散
- ランダム効果:研究内での分散 + 研究間での分散
となります。
分散を大きく見積もると、95%信頼区間は広がるため、より有意差は出づらくなります。
固定効果の利点と欠点
固定効果の利点を端的に述べると
- ランダム効果より統計学的に有意差がでやすい
- サンプル数の多い研究の結果が反映されやすい
といった傾向があげられます。
逆に固定効果の欠点をあげると
- 分散を狭く見積もっているかもしれない(偽陽性の可能性)
- 研究間のばらつきを無視している
といった点があげられます。
ランダム効果の利点と欠点
もちろんランダム効果も万能ではなく、利点と欠点があります。
例えば、利点として
- 研究間のばらつきを考慮している
- 固定効果より一般的には保守的
といった傾向があげられるでしょう。
しかし、ランダム効果も欠点があり、
- サンプル数の小さな研究の影響を受けやすいことがある
- 統計学的な検出力が低下する(偽陰性)
- 研究間のばらつきはランダムでないかもしれない
(つまり、異質性の原因となる因子(effect modifier)がある)
などがあげられます。
ランダム効果のほうが望ましいケースが多いです。
それでも「ランダム効果だから大丈夫」と安易に考えないようにしましょう。
まとめ
今回は固定効果(fixed effect)とランダム効果(random effect)について解説してきました。
次回は 出版バイアス(publication bias)について説明できればと思います。

おすすめ本はこちら
最初から読みたい方はこちら