Front-door adjustmentの実践（sequential g-estimation編）

前回こちらでフロントドア法（Front-door adjustment）について一通りの解説をしてきました。

こちらで概論については説明しましたが、

と疑問に思われた方もいるかもしれません。

疫学の分野でいう（g-method: g-computationやg-estimation）の概念が理解てき、実践できる方であれば、それほど難しい手法ではありませんので、今回、簡単に説明してみようと思います。

今回はsequential g-estimationを使用してやってみましょう。

Data generation processについて

まずは以下のDAGを想定してみましょう。

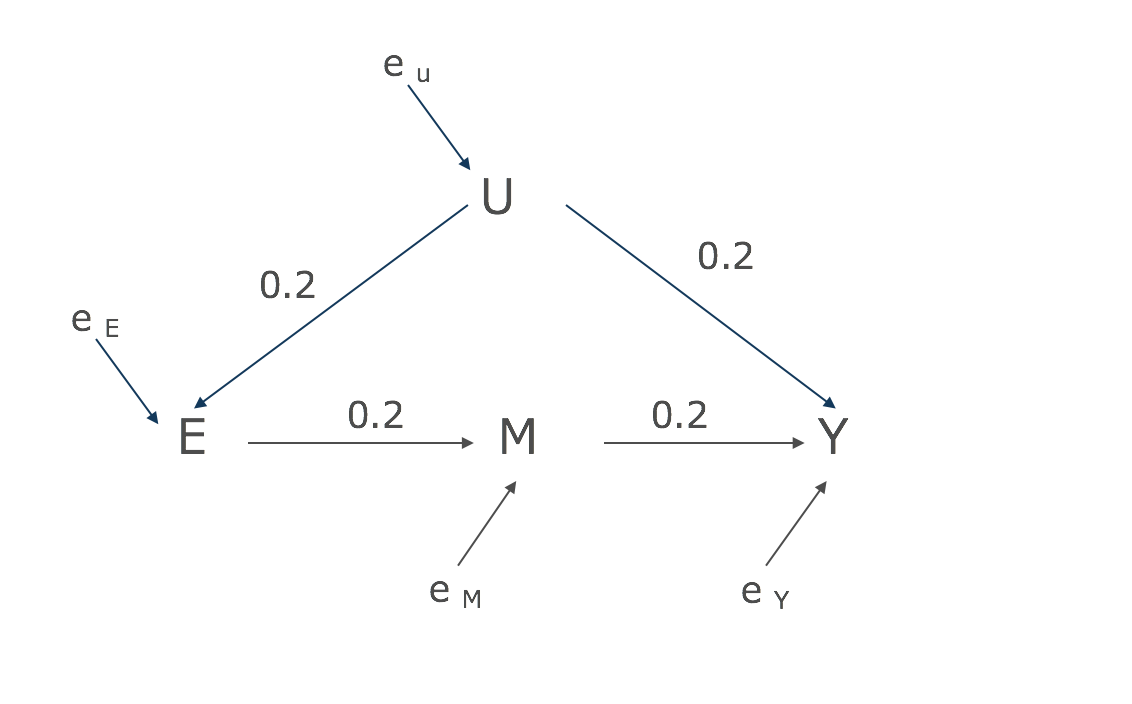
Structural equation model（SEM）を使用すると、

となります。10万例のサンプルでsimulationしてみましょう。

この状況で計測したい効果はE→M→Yになります。
Uはない状況です。どうやったら計測できるでしょうか？

この状況で使える手法には、

の２つがあり、今回は後者について説明します。

Sequentialは「連続した」などの意味があります。
つまり、ある手法で得られて予測値を使って、求めたい効果を計測する方法です。
そんなこと可能？と思った方がいるかもしれませんが、以下の例からみてみましょう。

まず、E→M→Yの効果をみようにも、Uが邪魔をして正しくみることができません。
例えば、E(Y|E)で回帰分析をすると

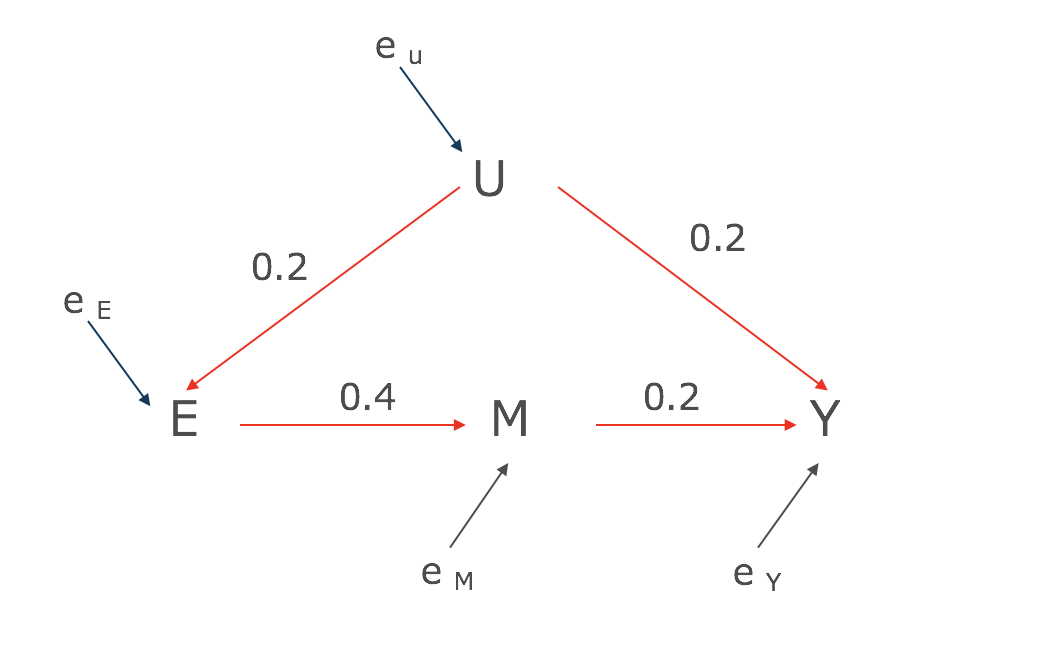
赤矢印の経路のように、

の２つの経路を合算した値（0.12）になってしまいます。

実際に統計ソフトでsimulation dataを回帰分析すると以下のようになります。

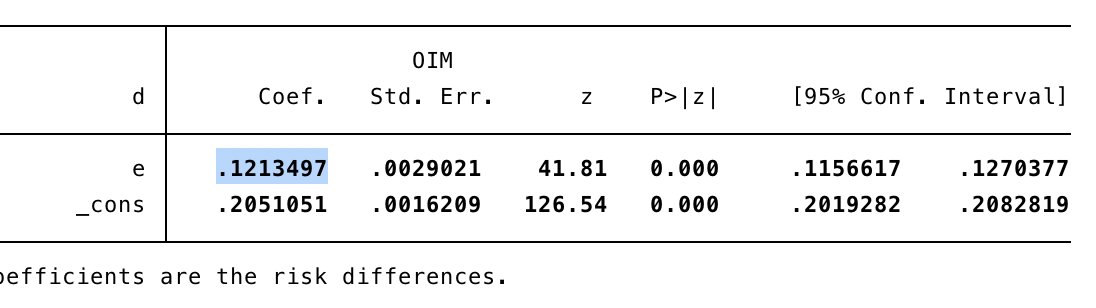
ある意味予想どうり、Risk Difference (RD) = 0.12となりました。

sequential g-estimationでは、この状況を２ステップで乗り越えます。

まず交絡因子を介した経路のみを推定してみましょう。

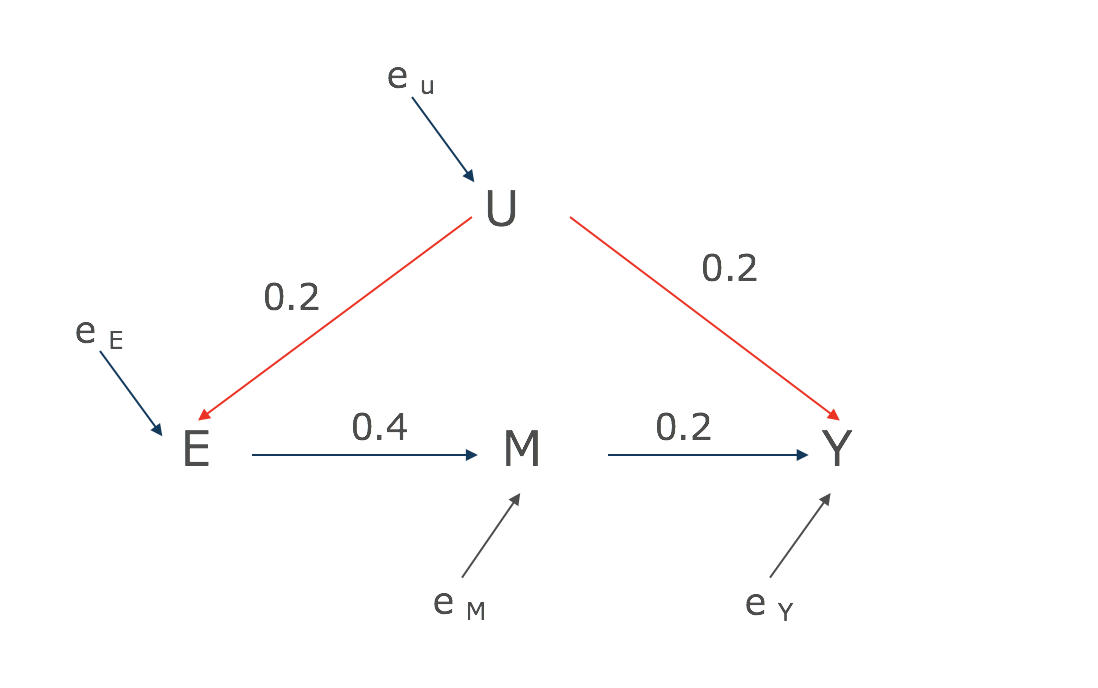
どうしたらこの赤矢印の経路がみえるかですが、Mをブロックしてしまえばいいのです。

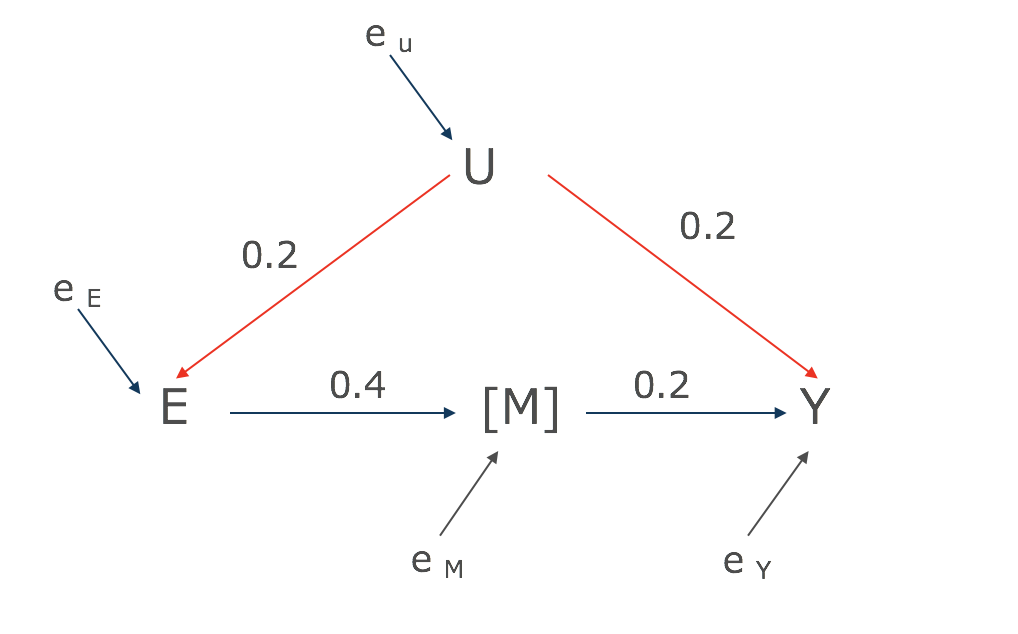
E(Y|M, E)と回帰分析をして、赤矢印を浮き彫りにします。
予測値としては、0.2*0.2 = 0.04です。

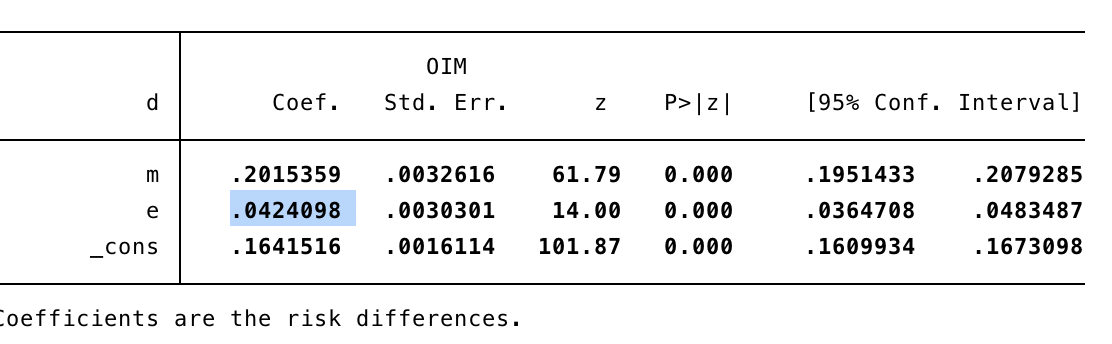
このアウトプットでわかるように、0.04となりました。

次に、Offsetを利用して、Uを介した経路を消し去り、YとEの治療効果をみます。

Offsetには、上のモデルのEのcoefficient（=0.042)にEを掛けたものを入れます。

そして、このoffset（OffD）を最後のGLMに入れて、YとEで回帰分析をします。
イメージとしては、以下のようになります。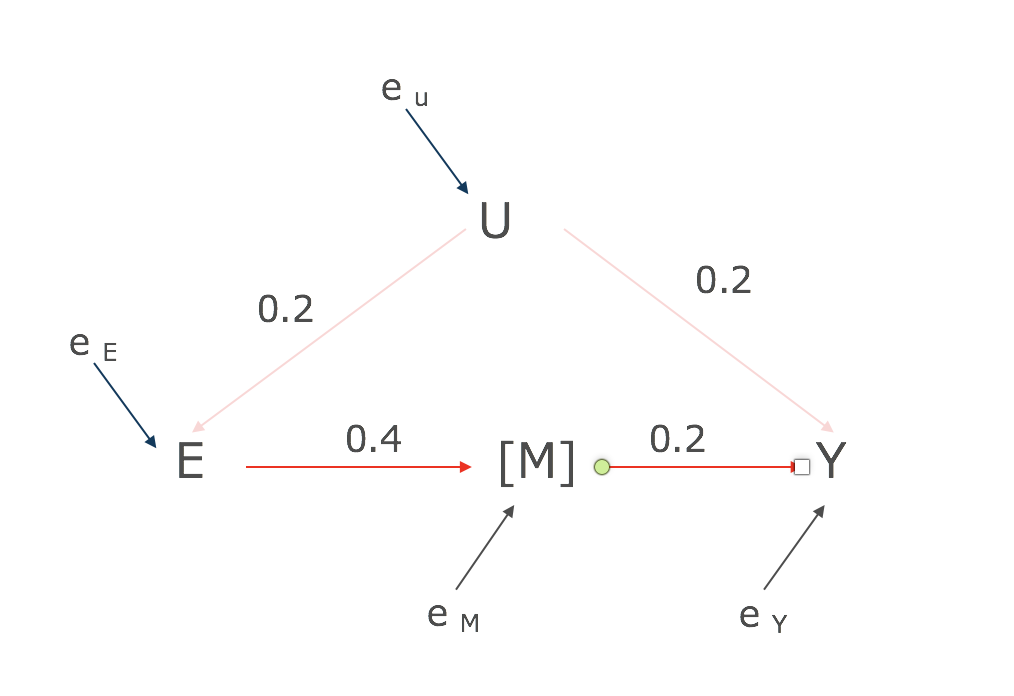

つまり、offsetを使用することで、E<–U–>Yの経路が消えてくれます。

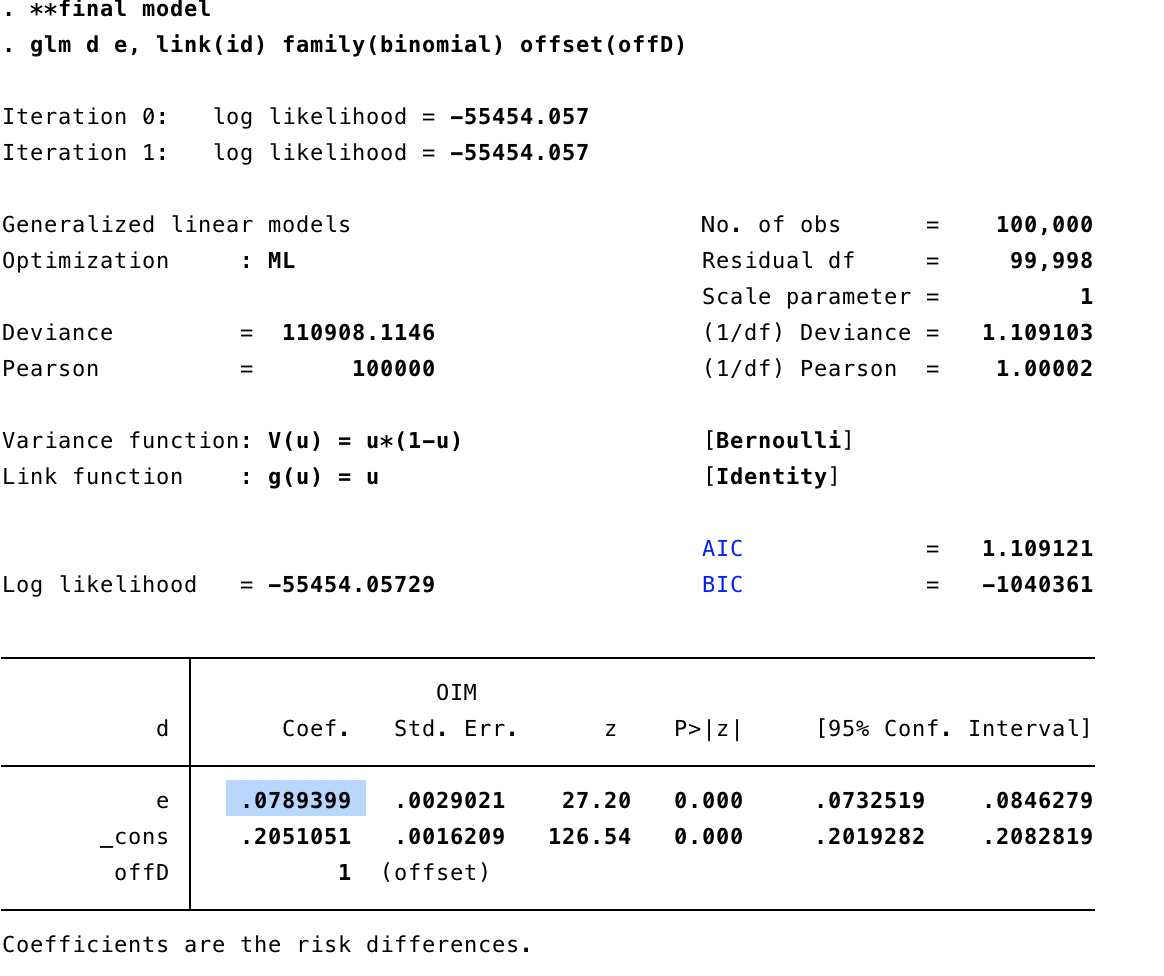
結果はRD = 0.0789となりました。
予測値は0.08ですから、ほぼ真の値に近づいています。

結果を見比べてみましょう。
単にYとEで解析した場合と、front-door adjustmentをした場合を並べてみます。

フロントドア	なし	あり
推定値	0.121	0.078

Front-door adjustmentを使用したほうが、推定値がかなり真の値（0.08）に近づいたのがわかると思います。

今回はfront-door adjustmentの方法を、sequential g-estimationを使用して推定してみました。
一見すると斬新な方法ですが、既存の手法の組み合わせで全然できます。

また機会があるときに、g-computationを使用した推定方法を説明できればと思います。