Affected sibling pair method、Case-Parent TriosとTransmission Disequilibrium Test (TDT)について[遺伝疫学]

今回は、non-parametric linkage analysisと呼ばれている手法について解説しいきます。具体的には、

• Affected sibling pair method
• Case-Parent TriosとTransmission Disequilibrium Test (TDT)

について解説していきます。

連鎖解析（linkage analysis）、LODスコア、Recombination fractionについて [遺伝疫学]今回は、Genetic linkage（遺伝的連鎖）の解析で必要な背景知識と、遺伝疫学で使用しているモデルとの関連を解説していこうと思い...

前回はLinkage analysisに必要な知識（recombination fraction: θ）や、LOD scoreの計算の仕方などを解説してきました。
LOD score linkage analysisにも欠点があり、別の解析方法についても知っておいて良いと思います。

LOD score linkage analysisの欠点

LOD score linkage analysisに欠点がなければ、わざわざ別の方法を覚える必要はないのですが、ほとんどの統計手法・疫学手法に欠点はつきものです。

この解析方法の欠点として、以下のような点が挙げられます：

• １人以上が罹患した家系が多数必要
• 片方の親がdouble heterozygote (AaBb)の場合が望ましい

これらの条件を満たせない（特に多数の家系のデータを集積する点）場合、別の手法を検討しても良いですし、２つ解析をして両方報告をしても良いわけです。

オススメの教科書は以下です：

Non-parametric linkage analysisについて

Non-parametric linkage analysisの特徴として、２人以上が罹患した核家族のデータを使用してlinkageの効果を統計学的に検定します。

LOD score linkage analysisのようにθ(recombination factor)は使用せず、IBD (identical by descent)という数値を指標に、シェアしているmarker alleleが予測値より高いかどうかを確認していきます。

IBD (identical by descent)は固定された事前確率

以下の表をみてください。

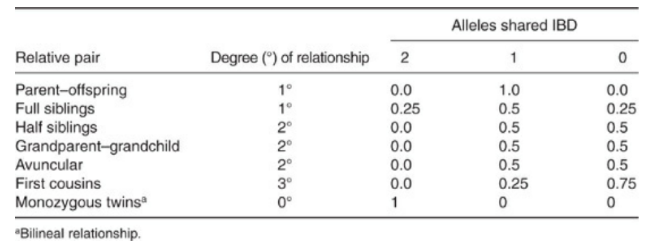
常染色体の遺伝子であれば、親子、兄弟などその関係性でIBDそれぞれの数値の起こりやすさ（確率）は数値として算出できます。

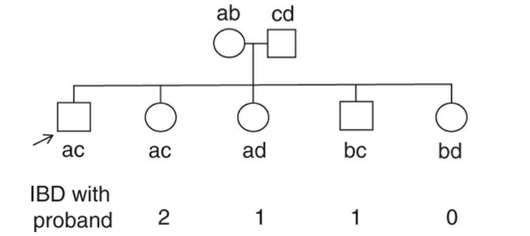
具体的に、heterozygoteの父母と子供４人の例で考えてみると、以下のようになります。

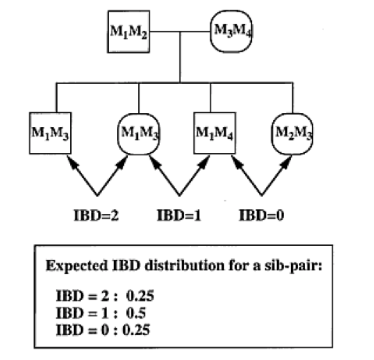
もし、罹患した兄弟などのデータを多数集めて、予測されるIBDの数（確率）より高ければ、そのmarkerは原因遺伝子とのlinkがあるのかもしれません。

Affected sibling pair (ASP) methodについて

罹患した兄弟のみを解析に行う場合、affected sibling pair (ASP) methodと言われます。
利点として、罹患した兄弟なので、研究に参加してくれる可能性が高かったり、データが集めやすいという利点があります。

また、この解析方法がnon-parametricと言われる理由ですが、疾患の遺伝モデルを指定する必要がないから”non-parametric”と呼ばれています。

このため、non-parametric linkage analysisは、より強固(robust)な方法として考えられています。

ASPの欠点

欠点としては、罹患した兄弟ばかりのデータを集めるため、そうでなかった兄弟の情報に触れる機会を逸してしまうことがあります。

また、特定のmarkerを使用してIBDを共有していた確率を算出し、未知の遺伝子が疾患と関連しているかを検定します。このため、未知の原因遺伝子を推定するのが困難なケースもあります。

 

Case-Parent TriosとTransmission Disequilibrium Test (TDT)

Case-Parent Trioとは、case（発症した子供）と両親２人を合わせたトリオのことを言います。

イメージとしては以下のようになります：

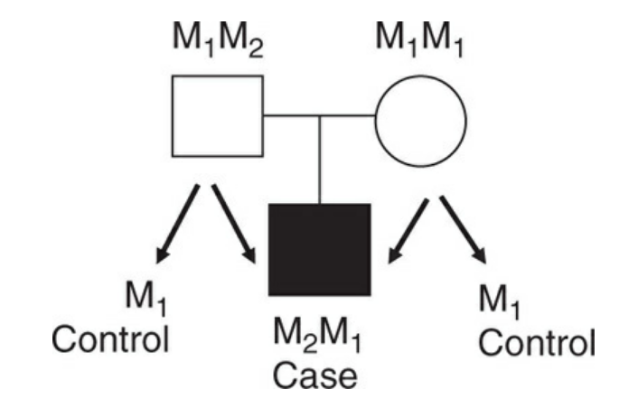
黒のCaseとその両親（M₁M₂とM₁M₁）です。
Caseと両親(Parent)の３人（Trio）のデータを使用して解析を行うため、Case-Parent Trioと呼ばれています。覚えやすくていいですね。

この解析ですが、とあるMarker（M: ２つのallele M₁とM₂）に興味がある場合に使用する方法です。今回の例でいうと、M₂と疾患の関連性を検討したい場合にこの方法を使います。

解析の前提として、両親の片方がM₁M₂のようにheterozygousである必要があります。

TDTの原理

Mendel’s law of equal segregation (メンデルの分離法則)であれば、M₁とM₂は等しい確率で両親から子供（疾患あり）へ遺伝します。

しかし、もしMと疾患の原因遺伝子に関連があれば、今回のケースでいうとM₂は疾患のある子供により遺伝していると予測できます。

帰無仮説(H₀)と対立仮説(H_A)

この現象を帰無仮説(H₀)と対立仮説(H_A)で説明すると、

• H₀: P(Parent transmits M₂|Parent is heterozygous M₁M₂) = 0.5
• H_A: P(Parent transmits M₂|Parent is heterozygous M₁M₂) > 0.5

となります。

これをLD（linkage disequilibrium: D）とθ(Recombination fraction)を用いた表現にすると、以下のようになります。

• H₀: D(1 – 2θ) = 0
• H_A: D(1 – 2θ) ≠0

つまり、帰無仮説が棄却された場合、marker (M)と疾患遺伝子の間に関連性(D≠0)とlinkage(θ≠0.5)があることになります。

このような表を作成します。

	# Transmitted Alleles
	M2	M1	Total
Observed	B	C	N
Expected	N/2	N/2

Nは疾患のある子供の遺伝子数の合計で、BはM₂、CはM₁のallele数になります。

そして、

• X²= [B – C]²/[B+C]

を計算し、chi-square検定を行えば良いのです。

TDTの例：Type 1 DM

一型糖尿病（T1DM）の例で考えてみましょう。

Case-Parent Trioの前提を満たす（片親がHeterozygote: Class 1/other alleles）家族を62組揃えたとします。

子供は62人で、その子のallele数は124個あります。
仮にClass 1 alleleが78個遺伝子、その他が46個だったとします。すると、以下のようなtableができます。

	# Transmitted Alleles
	Class 1	Other alleles	Total
Observed	78	46	124
Expected	124/2 = 62	124/2 = 62

 

このため、

• X²= [B – C]²/[B+C] = [78 – 46]²/[78+46] = 8.26

となり、P値を計算すると0.004となります。

よって帰無仮説は棄却され、marker (今回はClass 1 allele)と疾患遺伝子の間に関連性(D≠0)とlinkage(θ≠0.5)が示唆されます。

おわりに

今回は、LOD score method以外のLinkage analysesを解説してきました。

ASPやTDTは実際の論文では、もう少し複雑な解析方法になっていますが、ベーシックな点は非常にシンプルです。

オススメの教科書は以下です：