今回の論文は1997年、S Greenland教授がInternational Journal of Epidemiologyに投稿した論文です。
こちらの文献では論理 (logic) や帰納 (induction) を紹介しています。
特に、Popperian (Sir Karl Raimund Popper(イギリスの哲学者)を支持する人達の総称)らの「帰納 (induction)は不可能であり、存在しない」という主張に対する議論を行っています。
Greenland教授はこの議論は意味論であり、「帰納 (induction)は不可能」という批判は疫学者は注意して解釈する必要があると主張しています。
疫学者にとって、
- 帰納 (induction)は不可能が可能かどうか
- 帰納 (induction)は存在するのか
といった問題が議論の中心ではなく、疫学における因果推論で行う仮説において、確率論理(Probabilistic reasoning)をどう使用すべきかが中心になります。
はじめに
演繹(deduction)と帰納(induction)について先に簡単に説明しておきます。
演繹(deduction)とは、まず理論から入り、仮説を立て、観察をして確認するという流れにあります。つまり、
- Theory(理論)
- Hypothesis (仮説)
- Observation (観察)
- Confirmation (確認)
の順に論理が行われます。よく例にあげられるのがアリストテレスでしょう。
逆に、帰納(induction)はあるパターンを確認し、仮説を検証し、理論を想定することを言います。つまり、
- Observation(観察を重ね)
- Pattern (パターンを確認し)
- Hypothesis (仮説を検討し)
- Theory (理論を立てる)
という全く逆の論理作業を行います。例をあげるとすれば、少し俗っぽくなりますがシャーロックホームズです。
疫学・統計学におけるPopperianとnon-Popperian
1960-90年代に疫学者において、Popperian vs. non-Popperianで、観察研究における演繹(deduction)と帰納(induction)に関する議論が行われてきました。
| Popperian | non-Popperian |
| ・演繹は必要 ・演繹で十分 ・生物統計学で支持 |
・演繹は必要 ・演繹だけでは不十分 ・他の分野(疫学)で支持 |
簡単にこの議論を要約すると上のテーブルのようになります。
Popperianもnon-Popperianも演繹(deduction)は必要と意見が一致しています。
一方で、Popperianは演繹(deduction)であれば十分と考えていますが、non-Popperianはこれでは不十分と考えていました。
疫学者の中でも意見が分かれていましたが、その根底に
- 「帰納は不可能であり、存在しない(induction is impossible and that does not exist)」
という主張に対する誤解や無知から来ている可能性があります。
Karl Popperの時代に言われた「帰納(induction)」は現代のベイズ哲学を完全に反映したものではありませんし、不完全な理解のまま議論をすることで不協和音を出している可能性もあります。
こちらの論文では著者が演繹(deduction)と帰納(induction)について解説しています。
演繹(deduction)
演繹(deduction)というと、一般から特殊へ(general to particular)という思考法と言われています。
辞書などには、「一般的・普遍的な前提から、より個別的・特殊的な結論を得る論理的推論の方法」など記載されています。
この定義通りに使用されていないケースは日常では多々あり、例えば
- 「アスベストの暴露のため、ある労働者2人は中皮腫を発症した」
という前提から、「アスベストは時に中皮腫を起こすことがある」と演繹します。
しかし、この前提は「一般的・普遍的な前提」ではないですし、結論も「個別的・特殊的な結論」ではありません。例えば労働者2人に起こった事実が「一般的・普遍的な前提」とするのは少々無理があるのもうなづけるでしょう。
「普遍的な前提から、個別の結論を得る」という演繹は、論理的に考えてみて、前提の中に既に結論が入っています。別の言葉で言うと、演繹による議論では、前提の中にある情報を変換しています。
現代の論理では?
論文の著者は、dictionary of phyiosophyの言葉を借りて、
- 前提から結論を導く
- 論理的な必然性 (logical necessity)
という2点を強調しています。
つまり、「明確なルールの元、結論が前提に由来する」ことを議論することとしています。
仮説と観察からみた演繹(deduction)
ここで少し仮説(H)と観察(B)のルールを解説します。
- H: Hypothesis (仮説)
- B: Observation (観察)
としましょう。仮説(H)が、とある観察(B)を予測するのであれば、
- H implies B
- if H, then B
- B if H
となります。また、
- not H = 仮説が誤りである
- not B = Bとは異なるものが観察された
を意味します。
Modus ponens
Modus ponensは「肯定によって肯定する様式」などと言われるようですが、以下の論証になります:
- Premise 1: H implies B
- Premise 2: H
- Condusion: B
となります。分かりづらいかも知れないので、以下の図で考えてみましょう。
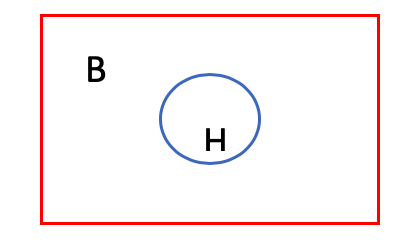
Hであれば必ずBが示唆されるのであれば、HはBの中にあります。(Premise 1)
もしHが正しいとあなたが知っていたら(Premise 2)、あなたはBを観測することになります (Condusion)。
Modus tollens
Modus tollensはこの逆を想定します。
- Premise 1: H implies B
- Premise 2: not B
- Condusion: not H
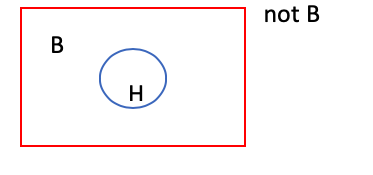
最初は同じく、HはBの中にあります。(Premise 1)。
もし、Bが正しくなければ(not B)、Hも正しくありません(not B)。
Deductive fallacies
Deductive fallacies(論理的誤謬)は、論理的な誤りのことを言います。例として、
- Premise 1: H implies B
- Premise 2: B
- Condusion: H
です。
仮説のが正しければ、Bが確認される前提で、Bを確認した。よって仮説は正しい。
一見すると正しい論証のように見えてしまいますが、図にしてみるとわかりやすいと思います。こちらの図を再度見てみましょう。

お気付きの方も多いと思いますが、仮にBを計測したとしても、Hの中の可能性も(H)、Hの外の可能性(not H)もあるわけです。
よって、Bを計測したからといって、仮説が正しくない(not H)の可能性があります。
Deductive fallaciesは科学でも生じている
- Hを研究の仮説
- Bを研究結果の観測
として考えていましょう。
とある研究者が、「仮説HはBを予測するであろう」と仮定しました。
彼が実験したところ、Bを観測しました。
よって「仮説Hは正しいはずだ」と主張しました。
つまりこの論証方法は、Deductive fallacieに当たります。
Defuctive fallacieの善し悪しは置いておいて、演繹(deduction)のみでは実際の研究で因果推論をするのが困難な点が示唆されます。
さらに疫学研究で考えてみましょう。
- 仮説(H): シリコンを使用しても強皮症は起こらない
- 観測(B): 統計学的に、シリコンの使用と強皮症は有意な関連がない
や
- 仮説(H): タバコは肺癌の原因である
- 観測(B): 統計学的に、タバコと肺癌は有意な関連がある
でも同じことが言えます。
なぜなら、仮にRCTを繰り返しおこなったとしても、交絡因子が残っている可能性があります。追跡中にドロップアウトが沢山生じて、選択バイアスが起こっていることもあります。実は盲検化が不十分で、計測エラーや誤分類といった情報バイアスが生じていることもあります。
とある「科学的な法則」で一連のイベントが起こっていたとします。しかし、起こってしまったイベントを計測するだけでは、「科学的な法則」を演繹(deduction)のみで導き出すことは困難です。
このことを「non-identifiable」や「non-provable」と言われています。
このため、前提(assumption)を受け入れて原因と結果について推論していきます。
例えば、疫学研究の例でいうと、
- 交絡が残っていなかったら
- 選択バイアスがなかったら
- 情報バイアスがなかったら
といった前提を受け入れて論理を展開していきます。
この論文の著者によると、実はPopper自身も演繹法(deduction)の限界の中での論証を行ってきましたが、他の哲学者たちが限界を受け入れていないのです。
帰納(induction)について
帰納(induction)は、様々な思想家や哲学者にとって取り組まれてきました:
- Bacon
- Whewell
- Mill
- Peirce
- Keynes
- Carnap
先ほど説明した「Deductive fallacies(論理的誤謬)」は「Induction(帰納)」のことであるとラベルを貼られてしまうこともありますが、著者によれば偏った考え方のようです。
帰納(induction)とは?
帰納(induction)は、「個別な事例から普遍的な法則を見出そうとする論理的推論の方法」などと言われています。
Deductive fallacies(論理的誤謬 or the Fallacy of Affirming the Consequent)も帰納(induction)法の論理に当てはまる節があります。
誤謬というとネガティブな印象を受けてしまいますが、繰り返し観察を繰り返すことで、予期せぬ仮説が浮かぶこともあります。このことをabductionやretroductionと呼んでいます。
このように帰納とretroductionを論証で使用する人にとって、演繹 (deduction)法が存在するか否かは重要ではありません。むしろ、真の前提から真の仮説を導き出し、仮説を妥当に反映させることにあります。
Popperの述べた帰納(Induction)
Popperは、帰納法による推論を「繰り返し観察した例から、まだ計測されていない例を推論すること(inference from repeatedly observed instances to as yet unobserved instances)」と述べています。
この定義は辞書とは、以下の点が異なります:
- 繰り返し観察する点
- 普遍的な仮説ではなく、まだ計測されていない例
という2点です。
つまり、繰り返し計測された例では、まだ計測されていない例や、その繰り返し観察された例を同時に予測する普遍的な仮説を議論しているわけではありません。
Popperは
- 計測された例を予測する仮説を立てる
- 仮説を利用し、まだ計測されていない例を演繹的に予測する
の2つのステップ言及しています。実際にこのステップで帰納(induction)を使用しているのは、(1)の仮説を立てる段階のみです。
さらに、Greenland教授は、「帰納は存在しない(induction does not exist)」を、
- 計測された例と計測されていない例に直接の関係は論理的にはない
- これらの関連性は、仮説を介して、間接的に関係している
と意訳しています。あるいは、
- 確信を持って、計測された事実から正しい説明を導き出す論証法はあるのだろうか?いやない。
とも解釈できると述べています。
統計学による帰納(Statistical induction)
統計学による仮説検定は「帰納的(inductive)」言われることがあります。例えば、
- 「significance-testingは帰納的な推論方法」(Fisher)
- 「仮説検定は、帰納的な行動方法」(Neyman)
- 「Bayesian approachは、帰納法による科学」(R von Mises)
と述べています。
Fisherのmaximum-likelihoodやBayseanの例から
例えば、母集団にランダムで抽出されたサンプル(N)において、ケースがA計測されたとしましょう。
この場合、疫学的には
- Prevalence(罹患率)= P = A/N
となります。これをFisherのmaximum-likelihood approachをすれば、A/Nは想定する母集団の罹患率を推定してことになります。
PLが2.5%ileでPUが97.5%ileとBaysianのPosterior distributionで考えると、
- Pr(PL < P < PU) = 0.95
となります。これは、サンプル集団、likelihood、事前確率から帰納された、母集団の罹患率(P)とも言えます。
Deductive induction
数学的な演繹法(mathematical induction)が最も有名な例です。例えば、
- Premise: S(1)
- Premise: S(n) implies S(n + 1)
- Conclusion: For all n, S(n)
となります。
少し言葉で説明すると、
- n = 1の時に、S(1)は正しい
- S(n)が正しい時は、いつもS(n + 1)が正しい
- どのようなnでも、S(n)が正しい
となります。この数学的な演繹法(mathematical induction)が疫学で応用されるケースは少なく、proabilitstic induction(確率的な演繹法)が使用されています。例えば、
- 統計解析の前提の1つとして、事前の分布を考慮する
- 事前の分布は、間違っている可能性もあるし、批判の対象ともなりうる
- その上で、Baysean estimationは、完全に帰納的な過程となる
です。
感想とまとめ
Greenland教授の真髄のような論文です。
この論文を何度も読んでいるのですが、まだ半分も理解できていないのかもしれません。ネイティブの方ですら「彼の文章は非常に読みづらい」「意味がわからない」「自分に酔っている」と評されていることもあります。
擁護するわけではありませんが、私はこれでいいと考えています。
なぜなら、彼の論文やModern Epidemiologyの文章はすべての人を対象に書いたものではありません。
疫学の導入本は他にもたくさんあり、彼の伝えたいことはそこではないからです。彼の論文も同じで、疫学初学の人への説明ではなく、方法論者を対象にしていることが多いです。
彼のような疫学の方法論者達が、疫学において哲学を展開し、新たな手法への意味付けをしてくれています。
もちろん、こちらの論文を読んで、すぐ明日に役立つ知識にはなり得ませんが、それでも原理原則にチャレンジする論文を読み、理解をしようとすることは必要です。