第７回：コホート研究における暴露の評価【グループ化、時間依存性の暴露、Induction Time, Immortal Person Time】

今回はコホート研究における暴露因子（Exposure of Interest）の評価方法について解説していきます。

コホート研究ときくと、『「暴露あり/なし」の２群にわけて…』と考えてしまいがちですが、これにもデメリットがあります。

そのほかにも、コホート研究で参加者を追跡すると、暴露の状況が変わってしまうこともあります。

今回はこれらを順番に説明していきたいと思います。

本記事の内容

暴露因子（Exposure）を固定する、変化を許容する
Lagged TimeとInduction Time
Immortal Person-time

前回はコホート研究の入り口と出口について解説してきました。
具体的には、Open Population, Closed Population, Fixed Population, とCensoringについてです。

第６回：コホート研究の入り口と出口【オープン vs. クローズドな集団と打ち切り】前回はコホート研究の概要について解説してきました。 https://www.dr-kid.net/entry-2018-12-01-0...

今回もModern Epidemiology（3rd edition）を基に記載していますが、直訳ではありませんし、私の解釈と背景知識を織り交ぜながらの解説になります。

今回も少しアレンジしていますので、ご容赦ください。

暴露因子を固定するか、変化を許容するか

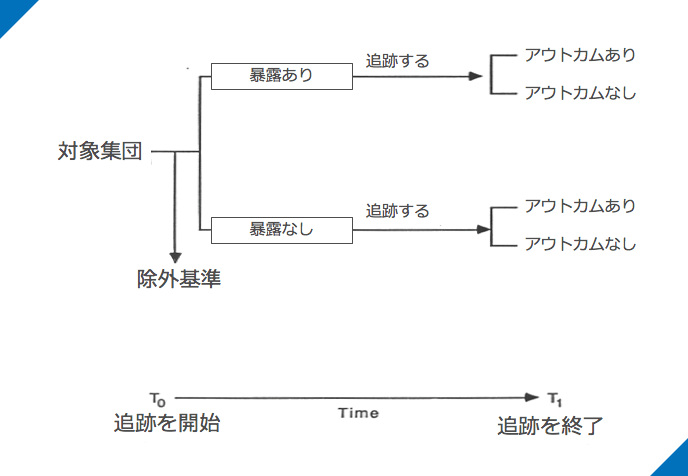
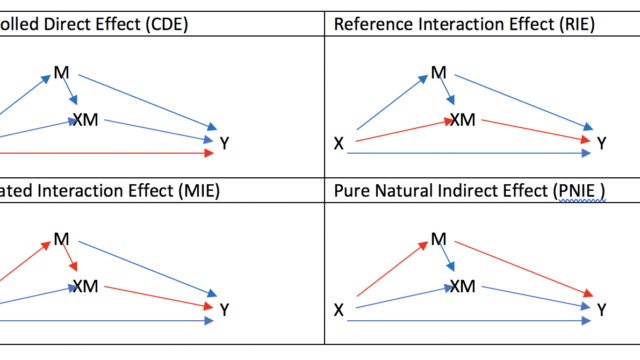
上の図の形式でいくと、

研究開始と同時に暴露を計測
追跡をし、アウトカムを計測する

となります。

この場合、１回しか暴露を計測しないため、固定することになります。
別の言葉でいうと、変化を許容しないことになります。

例えば、タバコを暴露因子にする場合、

喫煙したことがある
喫煙したことがない

の２群にわけることになります。

あるいは、これまでに吸ってきた量（Packs/ Year）で固定するケースもあります。

暴露因子を固定する場合、

これまで蓄積されてきた暴露の影響が永続する
暴露が途中で変わっても、量が増えても、影響は変わらない

という強い前提を置いていることになります。

「暴露あり/なし」の２群にするのは一見シンプルな方法ですが、その反面、非常に強い前提が必要になります。

暴露を固定しない場合

暴露因子（Exposure）を固定しない場合、追跡期間で問診をする度に同じ質問を繰り返すことになります。

例えば、

研究参加時の喫煙状態
研究参加２年後の喫煙状態

といった感じに、繰り返し同じ質問するをすることになります。こちらの方が実世界に即しているのは一目瞭然です。DAGを使って、この現象をみてみましょう。

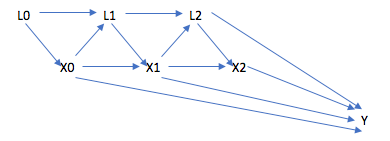
Xを喫煙、Lを交絡因子、Yをアウトカムとすると、上のDAGのようになります（やや簡略なDAGにしています。悪しからず）。

この場合、通常の回帰分析やPropensity scoreでは対応不可能で、

Inverse probability weightingによるmarginal structural model (MSM)
g-computation
g-estimationによるstructural nested model (SNM)

などの手法が必要になります。

（慣れてしまえば、それほど難しい手法ではありませんが、分からない方は、この手法をマスターしている専門家（統計家や疫学者）に依頼した方が無難と思います）

１つ定義をすることは、トレード・オフでもある

このように考えると、暴露因子の定義をすることは、表裏一体といえます。

つまり、シンプルに2群に分けると、情報量は減り、強い前提をおくことになります。
逆に、詳細に見ようとすればするほど、複雑なモデルや統計・疫学への深い知識が必要となります。

観察研究においてPECOやPICOをお勧めしない理由

臨床研究のセミナーなどでPECOやPICOのフレームワークを指導する講師が多いのですが、RCTならまだしも、観察研究でこのフレームワークを行うことは基本的にお勧めしません。

なぜなら、物事をシンプルにしすぎて、大事な情報を失ってしまうからです。

今回のように暴露を２群にし、変化を許容しないフレームワークを毎回のように行っていると、それが頭の思考回路で当たり前になってしまいます。

しかし、上にも述べたように、観察研究では暴露の定義１つをみても、非常に繊細です。

１つの解決法として、DAGの記載をお勧めします。

DAGであれば、時系列を考慮することもできますし、暴露（X）と交絡因子（L0）やアウトカム（Y）、中間因子（L1, L2）の区別もできます。

さらにDAGを使えば、IPWやg-computationの数式を作る際に役に立ちます。

現に、私は疫学研究の仕事をする上で、PICO/PECOは一度も使ったことがありません。（RCTのメタ解析の仕事を手伝う時を除きます）

Induction Time（Lagged Time）

さて、話を変えて、次はInduction Timeなどの説明をしていきましょう。

例えば、今日タバコを吸ったとして、明日すぐに肺がんになるわけではありません。
今日、CTによる放射線を浴びたからといって、明日に脳腫瘍ができるわけでもありません。

このように考えると、とある要因に暴露をしてから、一定期間を経てからアウトカムへの影響が出てくるといえます。

この「暴露してからアウトカムが生じるまでにかかる一定の期間」にまつわる用語で、

Lagged Time / Induction Time
Immortal Person-Time

という考え方があります。

Lagged Time/ Induction Timeについて

暴露してからアウトカムが生じるまでの一定期間のことを、Induction time（誘導時間・誘導期）と言います。

Lagged Timeもほぼ同じ意味で、暴露してからアウトカムまでにタイムラグがあるので、この期間のことを「Lagged Time」という方もいます。

どちらかといえば、前者（Induction Time）の方が馴染み深い方が多いでしょう。

Induction timeを考慮して、暴露因子を評価する

Induction timeを考慮して暴露因子を評価してみましょう。
今回はタバコが肺がんに与える影響を例にします。
例えば、とある人が

1970年：年間 50,000本のタバコ（7 pack-year）を開始
1975年：年間 50,000本のタバコ（7 pack-year）を継続
1980年：年間 150,000本のタバコ（21 pack-year）に増量
1985年：年間 150,000本のタバコ（21 pack-year）を継続

としましょう。
５万本/年 = 中等量、15万本/年 = 高用量と定義します（Modern Epidemiologyの定義のままです。実臨床と解離している点はご容赦ください）。
さらに、喫煙が肺癌に与える影響のInduction Timeは５年と仮定します。
さて、この４回の喫煙状況をどのように分類をしましょうか？

答えは、