ここ数年、「P値とはなんだろうか?」と考えさせられるような論文や記事、講演を多数、見聞きしてきたので、ここで少し考えをまとめておこうと思います。
普段、みなさんが読んでいる統計学の教科書とは少し考え方が異なるかもしれませんが、疫学的な考え方という点でご容赦いただければと思います。
「ここに記載されている内容に従うべき」という意味ではなく、近年、疫学の一部の先生方はこういった考え方をしていると紹介するのが意図です。
参考文献を最後に載せましたので、詳細について知りたい方はそちらを読んでいただければと思います。
仮説検定とP値の求め方
おさらいがてら、仮説検定の仕方とP値の求め方を簡単に解説します。
治療がアウトカムに有効であることを統計学的に評価する場合、平均や確率を2つ以上のグループで検定をする必要があります。例えば治療グループとプラセボグループでアウトカム(Y:平均)を比較する場合、以下のようなtableを作成する必要があります。
|
|
治療 |
プラセボ |
差 |
|
Y |
Y1 |
Y0 |
D = Y1– Y0 |
|
SD |
SD1 |
SD0 |
SDD |
帰無仮説(H0)と対立仮説(HA)は以下のように設定します:
- H0: Y1= Y0 つまり D = 0
- HA: Y1≠Y0 つまり D≠0
そして、帰無仮説を統計学的に棄却できるかを検定します。正規分布を仮定できるデータであれば、Z検定でき、Z-scoreは以下のように求められます。
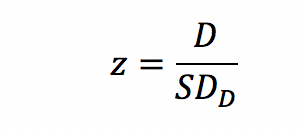
そして、最後にZ値の絶対値が、計測された値(D/ SDD)より極端になる確率を求めます。
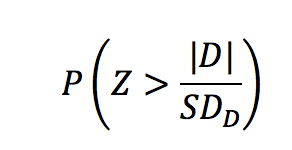
多くの場合、有意水準(α)は0.05に設定されています。
疫学的なP値の考え方
空想上のコホート研究になりますが、とある曝露因子が疾患の発症に関与しているかを検討していたとしましょう。
この研究では差(Risk Difference(RD))が0.30、標準偏差0.15でした。
帰無仮説(H0)と対立仮説(HA)は以下のように設定します:
- H0: RD = 0
- HA: RD≠0
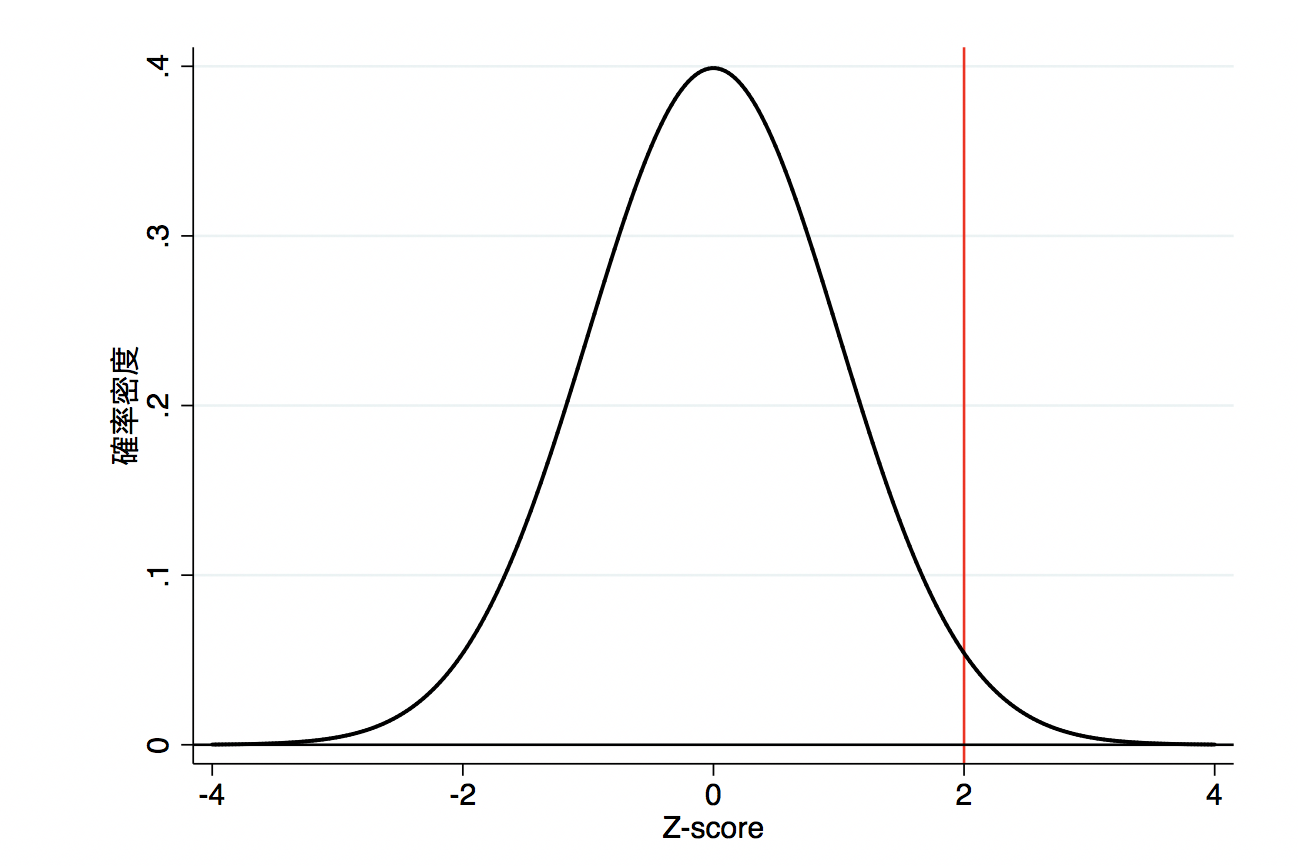
正規分布を仮定して、Z値を計算するとZ = 0.30/0.15 = 2.00で、P値は約0.05となりました。
さて、このP値(=0.05)の解釈はどのような解釈になるでしょうか。P値について学習した環境により、様々な回答が得られると思います。例えば、
- P値が0.05以下なので、曝露因子と疾患の発症に関連がある
- RDが0.30と偶然なる確率は0.05である
- RD = 0.30を計測する確率は05である
- Z = 2.00を偶然に計測する確率は05である
などが挙げられます。しかし、どれも間違いだらけです。
例えばこの解釈をModern Epidemiology1に準拠して説明をすると、
「帰無仮説が正しく、研究にバイアスがなく、使用した統計モデルに誤りがない場合に、Z値が2.00以上(Z-score >2.00)になる確率は0.05である」となります。
少し追加で解説をすると「帰無仮説が正しい」とは、RD = 0のことを指します。つまり、仮に2つのグループで差がなかった場合に(Z=0)、今回計測された値(Z=2)がどのくらいより極端なのかをみています。
よく統計学の本などにはP値は「帰無仮説が真のときに、統計的要約が実際の観測結果以上になる確率」などと記載されています。しかし、実際には「研究にバイアスがなく、使用した統計モデルに誤りがない」という点が省略されている点に注意が必要です1。
バイアスとは?
「研究のバイアス」とは、交絡・選択バイアス・情報バイアスの3つがメインです。これらのバイアスがある場合、P値だけでなく、点推定(point estimate)、95%信頼区間といった指標も信頼できないものになります。ですので、研究結果にバイアスがないという前提が実は必要なのです。

統計モデルが正しいとは?
また、仮説検定では2グループ以上を比較することになりますが、正しい「統計モデル」を使用する必要があります。例えば、正規分布していないデータで、Z検定をしても正しい結果は得られません。
例えば、正規分布モデルを使用して、サンプルサイズが小さい(N = 20~30)のデータを解析する場合を考えましょう。 母集団の大半が正規分布していないデータに従っていない場合、解析自体が妥当なものとはなりません。 また、母集団の大半が正規分布にほとんど従っているが、一部が外れ値の場合(飛び抜けた値)、サンプルサイズの小さいデータでは例外を見逃してしまうリスクが無視できなくなりますし、正規分布モデルを使った統計分析の誤差は、必要以上に大きくなるリスクがあります。
一方で、平均の解析では、中心極限定理により「母集団分布が正規分布」と仮定を緩めても、誤差は実用範囲におさまる可能性があります。
P値は本来は連続した値で、0.05以上/以下で二分することには再考が必要
また、P値とは連続した値です。伝統的に0.05を統計学的な有意水準としてきました。すると、P < 0.05であれば統計学的に有意となり、P > 0.05であれば有意ではなくなります。
しかし、本来、P値が0.049でも0.051でも、この差はほとんど意味がありません。
しかし、現実の研究論文や査読では、P = 0.049 をP値が0.05以下なので重要であるとし、P=0.051はP値が0.05以上なので重要でないと過度に単純化してしまっていることがあります。
この認知上でのバイアスを取り上げた論文もあります2。
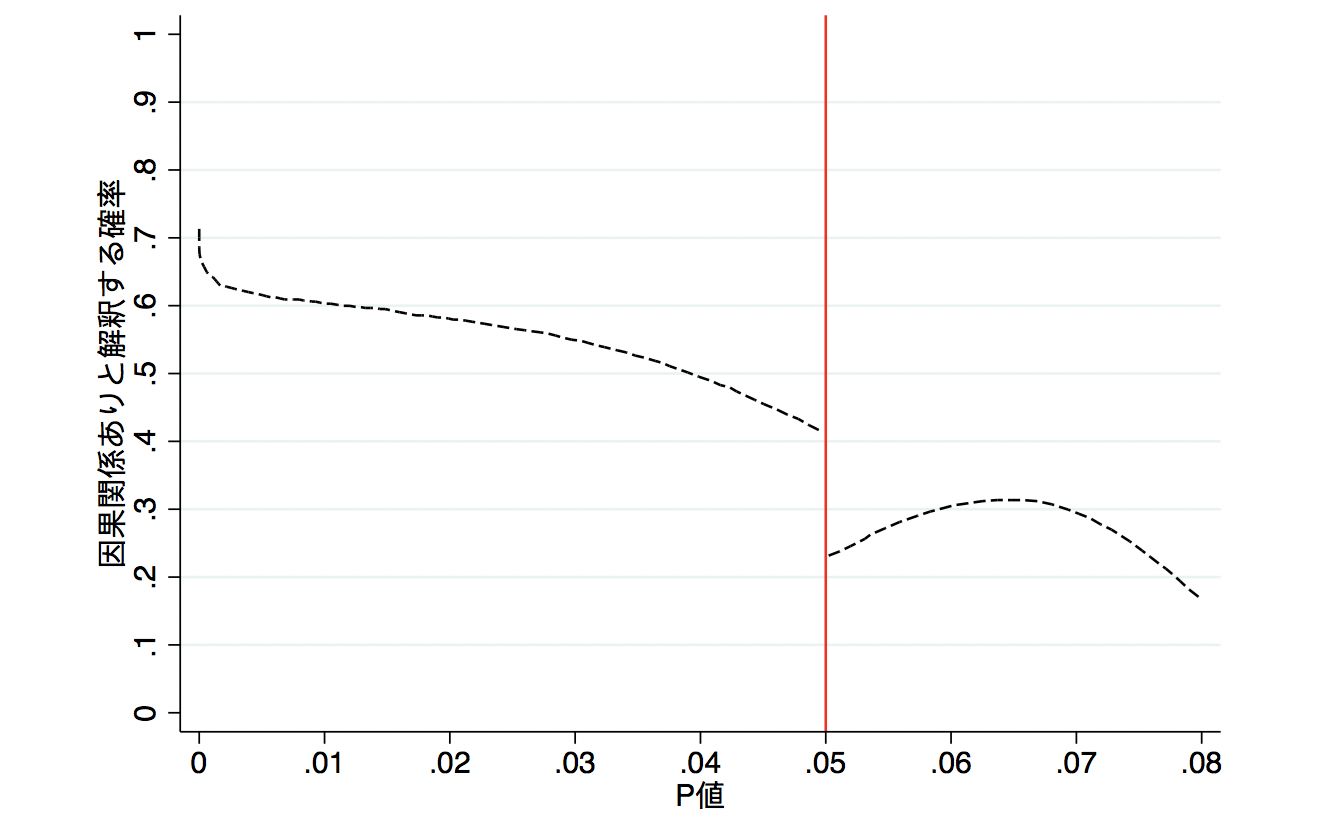
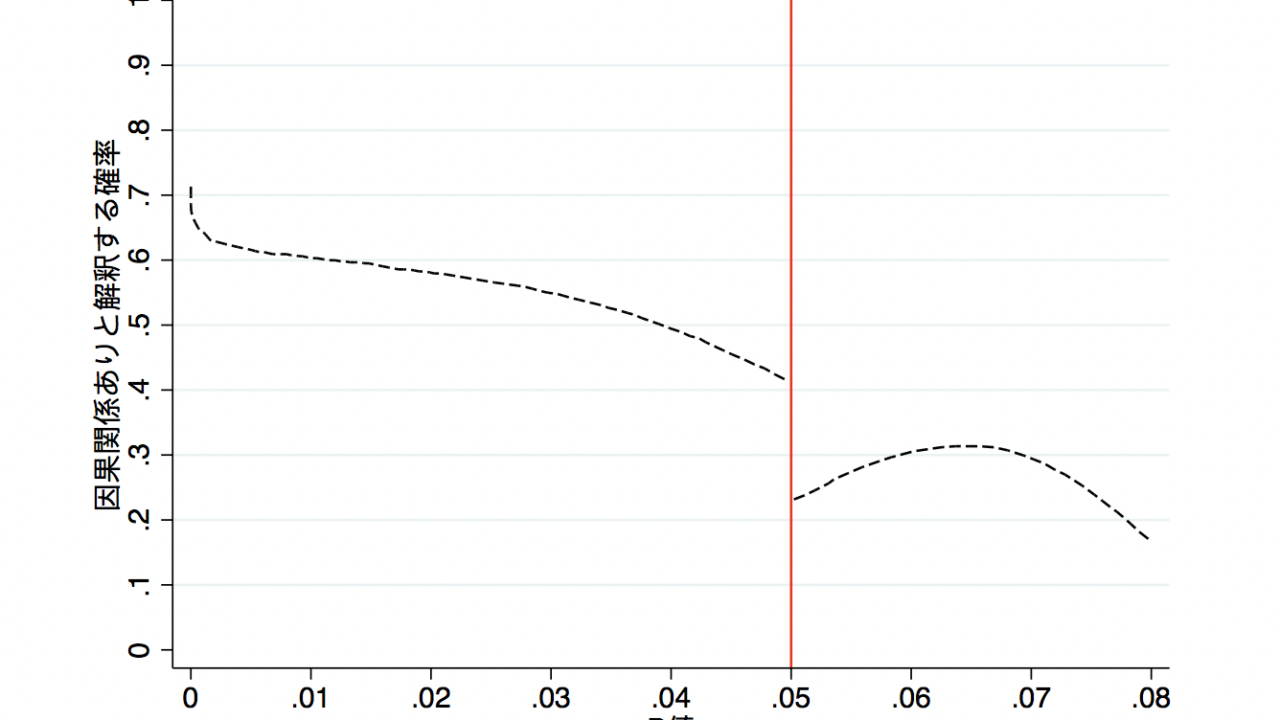
P値は0.049でも0.051でも、計測された結果の解釈に大きな影響があってはなりません。しかし、なぜかP値が0.05を下回った瞬間に「計測された結果(例:治療とアウトカムの関連)には、因果関係がある」と判断する確率が跳ね上がっています。
こちらの調査はオーストラリア疫学協会の会員を対象に行われた研究です。統計学や疫学のトレーニングを受けている方でも、P < 0.05というカットオフに踊らされている状況です。P値を有意か否かに二分して判断してしまう弊害がここにあります。
95%信頼区間について
P値とセットで報告されることが多いのは信頼区間です。
有意水準を0.05にした場合、95%信頼区間が報告されることが多いでしょう。一方で「信頼区間の上限/下限が帰無(OR = 1、RR = 1やRD = 0)をまたいでいなければ、統計学的に有意であり、関連性がある」 or 「またいでいるので統計学的に有意ではないので、関連性はない」といった解釈をしている方もいます
- 95%信頼区間が帰無をまたいでいる
- 統計学的な有意差はない
- 治療・介入効果がない or 関連がない
という3つのパートの分けて考えてみましょう。
「95%信頼区間が帰無をまたいでいるから、統計学的な有意差はない」という(1)→(2)は正しいです。
ただし、「統計的に有意である」という定義は「P値が前もって決めておいた有意水準α(多くは0.05)未満になる」に過ぎません。
医学論文の執筆や解釈では「(統計学的に)有意である」というニュアンスを入れて考えず、『単に「P値 < α」が成立しているだけ』と解釈するのみに留める必要があります。「統計学的な有意差あり/なし」の科学的意味は別に考える必要がある点に注意しましょう。
(2)→(3)の「統計学的な有意差はない = 効果なし」にあたりますが、これは誤りであることがあることがあるので、注意した方がよいでしょう。実際には、サンプル数が小さいため統計学的な有意差はないものの、治療効果を認めるものもあります。
- 95%信頼区間が帰無をまたいでいる
- 統計学的な有意差はない
- 治療・介入効果がない or 関連がない
をセットで解釈してしまい、「95%信頼区間とは何か?」を考えないと「P < 0.05は統計学的有意差があり、P > 0.05は有意差なし」という先ほどの単純思考と全く変わらなくなってしまいます。
ここからは、95%信頼区間の解釈について解説していきましょう。
95%信頼区間とは?
95%信頼区間の正しい意味ですが、使用した統計モデルが正しく、バイアスがない場合に「理論上、研究を無限に繰り返した場合、95%以上の確率で真の値を含む範囲(CI contains the true parameter with a frequency no less than its confidence level over hypothetical repetitions of the study)」のことをいいます。なかなか直感的に理解をするのが難しいと思うので、以下の図をみてください。
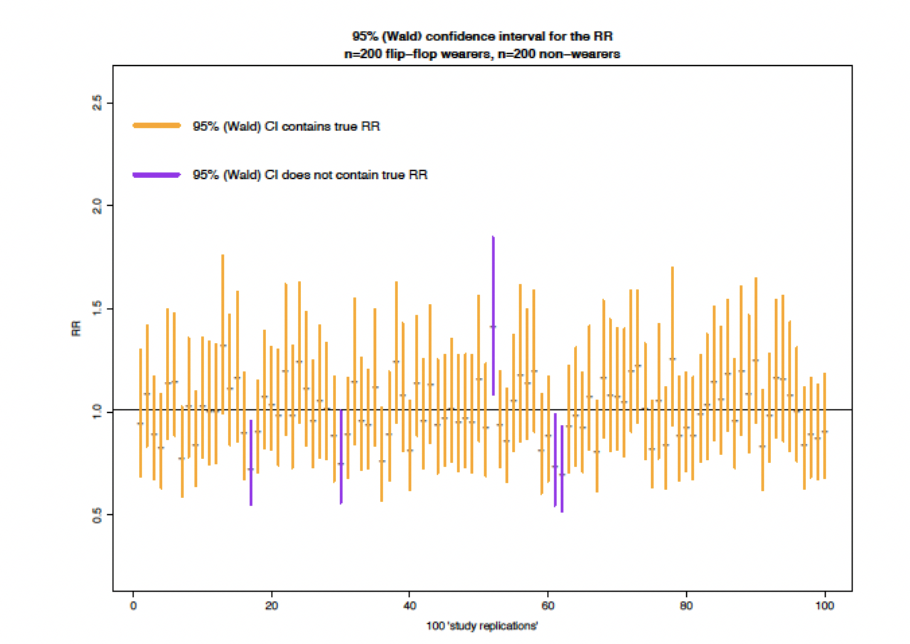
理論上の話ですが、100回研究を繰り返した場合、95回以上は真の値(今回はRR = 1.0)を含んでいる区間が95%信頼区間といえます。こちらのシミュレーションデータでは、ちょうど95回は真の値を含んでおり、5回は真の値を含んでいません。このような区間を95%信頼区間といいます。
95%信頼区間の問題点としては、たとえば行われた研究が真の値を含んでいるのか(オレンジ)、含んでいないのか(紫)、誰にもわからない点です。このため、たった1つの研究では確定的なことはいえないのです。
また95%信頼区間はサンプル数やデータのばらつきにも影響を受けます。例えばサンプル数(患者数など)が多く、データのばらつきが少なければ、それだけ95%信頼区間は狭くなり、より正確な推定が可能となります。
まとめ
今回はP値と95%信頼区間について解説してきました。どちらも思ったより直感的でないし、少し理解しづらいと感じている方が多いかもしれません。
しかし、単純化してしまうことで、本来のP値や95%信頼区間のもつ意味が変わってしまうことがあります。例えば、P値を「偶然おこる確率」と端的に言って、P < 0.05なら有意であるとしてしまうと、P < 0.05なら有意で意義があると極端な思考になってしまいます。
次回は、P値とダイコトマニアについて考えていこうと思います。
参考文献
- Rothman, K., Greenland, S. & Lash, T. Modern Epidemiology, 3rd Edition. (Lippincott Williams & Wilkins., 2012). doi:8184731124
- Holman, C. D. A. J., Arnold-Reed, D. E., De Klerk, N., McComb, C. & English, D. R. A psychometric experiment in causal inference to estimate evidential weights used by epidemiologists. Epidemiology12, 246–255 (2001).
黒木玄さんのtwitter上でのコメントも参考に、記事を訂正しています(以下リンク)。コメントありがとうございました。
#統計 再度、コメント。
世界的に標準化された教科書的な(統計学入門の分野では、ゆえに悪い)解説の影響のせいで、説明がクリアでない点が多いと思いました。
実践的に使う数学的道具の説明では、その道具が使用可能になる前提条件が現実にどれだけ成立しているかの説明が必須だと思いました。続く https://t.co/7rxCV5WSzW
— 黒木玄 Gen Kuroki (@genkuroki) January 2, 2020