今回はこちらの論文をピックアップしました。
今回はGreenland教授の記載した確率の論理(probabilistic logic)について記載しています。
近年、因果推論が徐々にブームになってきていますが、因果推論におけるPotential Outcomeのフレームワークを理解するにも、確率の論理のベーシックな部分の理解が非常に重要です。
特に疫学のトレーニングを受けるのであれば、確率の論理を理解した上で統計モデルや因果推論のモデルを考える必要があります。
原著論文を直訳するとカオスになるため、ここでは必要な確率の公理(axiom of probability)と、それを実際に疫学研究でどのように活かしているのかの実例も記載していきます。
Axiom 1: Non-negativity
最初の公理(axiom)はnon-negativityです。
意味はそのままで、確率は0以上になります。
- 0 ≤ P(A)
Axiom 2: Tautology
2つめのAxiomは、Tautologyです。
Tautologyの解釈ですが、
- 常に無条件的に真である
- 論理的に避けることのできないイベント
です。例えば、「A = 95%信頼区間が真の値を含む or 含まない確率」と言えばTautologyで、当然「P(A) =1 =100%」になります。
また、Axiom 1と2を合わせると「0 ≤ P(A) ≤ 1」となります。
Axiom 3: Mutually Exclusive
Mutually exclusiveとは、 相互に排他的な事象などと日本語で言われているようです。
AとBがMutually exclusiveであれば、AまたはBが起こる確率は、Aが起こる確率とBが起こる確率の和になります。つまり、
- P(A or B) = P(A) + P(B)
となります。
Axiom 4: Conditional Probability and Independence
4つ目はConditional Probability(条件付き確率)とIndependence(独立)です。
Conditional Probability(条件付き確率)について
AとCが別の異なるイベントで、Cが生じた後にAが起こる確率は、以下のように表記できます。
- P(A|C): Probability of A given C
さらに、これはCが起こった後に、AとCを確認するのと変わりがないため、以下の等式が成り立ちます。
- P(A|C) = P(A, C)/P(C)
例えば以下の例で考えてみましょう:
袋の中にボールが100個あったとします。
- 60%は赤色 (A = 1)、40%は青色 (A = 0)
- 30%は赤色(A = 1)かつ小さなボール(B = 1)でした。
これを数式に変換すると、
- P(A=1) = 0.6
- P(A=1, B=1) = 0.3
となります。よって、赤いボールうち、小さいボールである確率は、
- P(A=1|C=1) = P(A=1, B=1)/P(A=1) = 0.5
と50%となります。
Independence(独立)について
ここでは、Independence(独立)についてまず説明します。
Independenceとは、AとBという2つのイベントがあり、AがBを予測しない、BがAを予測しないことを言います。
Independenceにも、
- Marginal Independence
- Conditional Independence
の2種類があります。
Marginal Independenceについて
Marginalとは「全体の」と行った意味があります。
つまり、サンプルした集団全体において、
- AがBを予測しない
- B=1 とB = 0に分けても、Aが起こる確率は変わらない
- Bの情報は、Aの予測に役に立たない
などと言い換えることができるでしょう。
AとBが独立している場合、以下の等式が成立します:
- P(B|A) = P(B)
- P(A, B) = P(B|A)P(A) = P(B)P(A)
最初のP(B|A) = P(B)ですが、AがBに影響を与えないので、Aの情報があっても、なくてもBが起こる確率は変わりません。
このため、P(B|A) = P(B)となります。
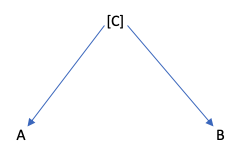
DAGとリンクさせて理解すると良いかもしれません。AとBが独立しているDAGとは、例えば以下の例が代表的です。
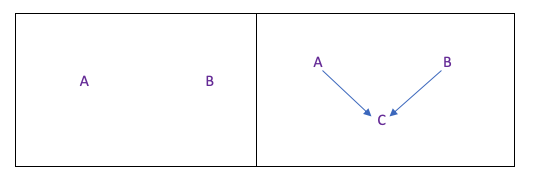
例えば、左側のようにAとBを結ぶ矢印がない例です。
AとBを結ぶ矢印がないので、当然ですが独立しています。
右側のDAGでも、AとBは独立しています。
なぜなら、AとBの共通の結果(a common result)の場合、AとBは独立したままになります。
この場合、CのことをCollider(合流点)と呼んだりします。
Conditional Independenceについて
次に、Conditional Independenceについて考えてみましょう。
Conditional independenceは、とある条件(C)においてAとBが独立した状態と言えます。例えば、Cという条件化であればAとBが独立しているというと、
- P(B|A, C) = P(B|C)
- P(A|B, C) = P(A|C)
となります。
実際の疫学研究では、C = 0 とC = 1に分けてA vs Bを見た場合、AがBを or BがAを予測しない状態とも言えます。
これをDAG上で書くと以下のようになります:
この場合、CはAとBの共通の原因とも言います。このCを疫学では交絡因子(confounder)と言ったりします。
つまり、Cを層別化したり、回帰分析のモデルに組み入れることで、AとBの関連性が切断されます。
このように統計学的に対処した時、DAG上では変数を四角で囲ったり、[ ]を使用して表現します。
Harvard大学などで四角を囲う文化であり、PearlやGraanland教授のいるUCLAなどの流派ではカギ括弧 [ ]で表現しています。
どちらも本質的には変わりません。
Axiom5: Joint Probability
Joint probabilityは、同時分布などと言われることがあります。
例えば、AとBが同時に起こる確率は、
- P(A, B)
と記載します。このことをJoint probabilityと言います。
Chain ruleについて
Chain RuleはJoint probabilityをConditional Probabilityに簡単に変換する方法で、
- P(A, B) = P(A|B)P(B)
- P(A, B, C) = P(A|B, C)P(B|C)P(C)
- P(A, B, C, D) = P(A|B, C, D)P(B|C, D)P(C|D)P(D)
などとなります。
Law of total probability
Marginal probabilityをConditional probabilityに変換したりする際に使用します。
例えば以下の等式が成立します:
- P(A)
- = Σb P(A, B)
- = Σb P(A|B)P(B)
また、以下のように2つのイベントを加えることも可能です。
- P(A)
- = Σb, c P(A, B, C)
- = Σb, c P(A|B, C)P(B|C)P(C)
Axiom 6: Bayes’ rule or Inversion formula
最後は有名なベイズルールです。実はBayes’ ruleも、これまでのAxiomから証明できてしまいます。
- P(A|B)
- = P(A, B)/P(B)
- = P(B|A)P(A)/P(B)
- = P(B|A)P(A)/[ΣaP(B, A)]
- = P(B|A)P(A)/[ΣaP(B|A)P(A)]
これをH = hypothesis, B = Observationとして、同じことをしてみましょう。
- P(H|B) = P(B|H)P(H)/P(B)
となります。
P(H|B)は、posterior probability(事後確率)と言います。
P(B|H)は、Hのlikelihoodと呼びます。
P(H)は、propr probability(事前確率)と言います。
Exercise:練習問題
少し練習問題を記載しておきます。
Axiom 1-6を理解していれば、簡単に解ける問題です。
Exercise 1
- P(A, B, C|D)において、Aをアウトカムとする条件付き確率に変換しましょう
答えは以下の通りになります
- P(A, B, C|D)
- = P(A, B, C, D)/P(D)
- = P(A|B, C, D)P(B|C, D)P(C|D)
Excercise 2
- DにおいてAとBが独立だったとします: A ||B | D
A is independent of B given D - P(A, B, C|D)において、Cをアウトカムとする条件付確率に変換しましょう
答えは以下の通りになります
- P(A, B, C|D)
- = P(A, B, C, D)/P(D)
- = P(C|A, B, D)P(A|B, D)P(B|D)
- = P(C|A, B, D)P(A|D)P(B|D)
ポイントは、Dという条件下では、AとBが独立しているため、
- P(A|B, D) = P(A|D)
になるという点で、3つ目から4つ目の変換が可能となっています。
Exercise 3
- DとEは独立している場合、以下の等式が成立するか?
- P(C, D, E) = P(C|D, E)P(D)P(E)
答え
- P(C, D, E)
- = P(C|D, E)P(D|E)P(E)
- = P(C|D, E)P(D)P(E)
よって正しい。
ポイントはP(D|E) = P(D)となる点ですね。
Exercise 4
- Cという条件下でDとEは独立である場合、以下の等式は正しいか?
- P(C, D, E) = P(D|C)P(C|E)P(E)
答え
- P(C, D, E)
- = P(D|C, E)P(C|E)P(E)
- = P(D|C)P(C|E)P(E)
よって正しい。
ポイントはconditional independenceですね:
- P(D|C, E) = P(D|C)
疫学研究でaxiom of probabilityをどのように役立てているのか?
多くの方は、これまでに紹介 & 証明してきたaxiom of probabilityが、「実際に何に役に立つの?」とか、「これを覚える意味があるの?」と感じている方が多いと思います。
また、実際に健康のデータを取り扱っている疫学者や統計学者でも、これがどのように活かされているのか、曖昧なまま解析をしている人も多数います。
これから、どのように活かされているのか、実際の解析を例にして紹介します。
具体的には、
- DAGを読むのに必要
- Inverse probability weightの計算に必要
- g-formula (backdoor formula)の理解に必要
- Bias analysesで必要
と様々な解析の証明に必要な公式なのです。
DAGから確率を考える
DAGは因果推論を行う上で必要ですが、DAGを読み解き、自分の持っているデータに照らし合わせて考えるときに、確率と数式に変換する必要があります。
別の言葉で言うと、DAGはdata generation process (Dataがどのように構成されているのか)を考える上で必須なツールとも言えます(これはJ Pearl的なアプローチです)。
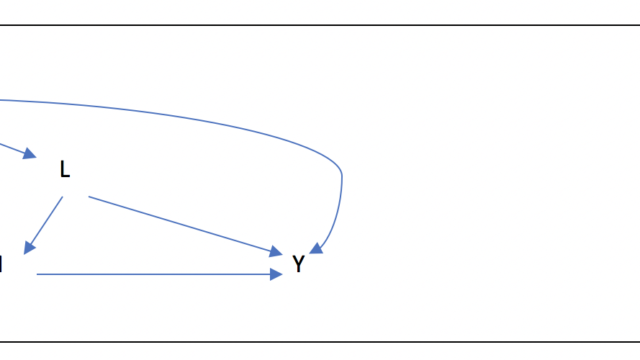
例えば、以下のDAGを見てみましょう。
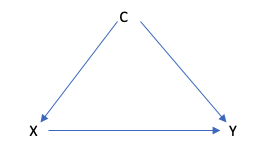
これを確率に変換すると以下のようになります:
- P(Y, X, C)
- = P(Y|X, C)P(X|C)P(C)
このDAGから
- YはXとCに影響される
- XはCにのみ影響される
- CはXやYには影響されない
という3つの情報が詰まっています。これがdata generation processを考えると言います。
Inverse probability weight (IPW)を考える
あまり知られていないことですが、DAGを正しく記載すれば、正しいIPWを導き出すことができます。

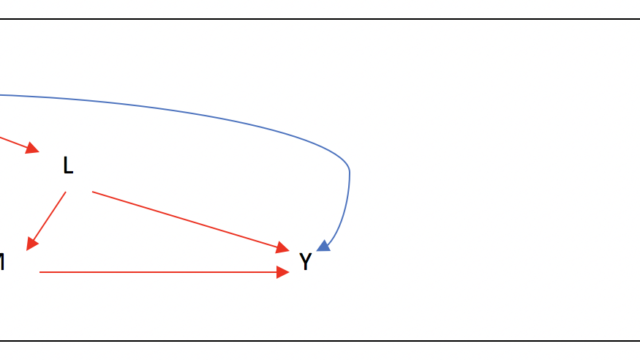
例えば、こちらのDAGは以下の数式で表せました:
- P(X, Y, C) = P(Y|X, C)P(X|C)P(C)
一方で、IPWではCからXに伸びている矢印を消したいので、以下のようなDAGを想定します(これをinterventional DAGと呼びます)。
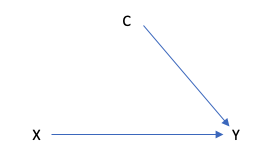
これを数式に直すと、
- P*(X, Y, C) = P(Y|X, C)P(X)P(C)
となります。CからXに伸びている矢印が消えたため、P(X|C) = P(X)に置き換わっています。
最後にIPWを計算してみましょう。
IPWは、(Interventional DAG)/(Original DAG)で計算できるため、以下のようになります。
- IPW
- = P*(X, Y, C)/P(X, Y, C)
- = [P(Y|X, C)P(X)P(C)]/[P(Y|X, C)P(X|C)P(C)]
- = P(X)/P(X|C)
となります。このP(X)/P(X|C)がstabilized IPWです。
*「1/P(X|C)やpropensity scoreの逆数を重み付けするのがIPW」という考え方もありますが、近年の疫学のmethodologistは、この考え方はIPWの本質を捉えておらず否定的でいる人もいます(私もそうで、PSの逆数のみをIPWに使うことは、まずあり得ません)。なぜなら、data generation processを無視していますし、DAGにおける妥当性の評価を怠っているからです。さらに、time-varying treatment/confounder, IPCWやIPSW、transportabilityの公式を考える時にも、困難になるケースがあるからです。
g-formula (backdoor formula)を考える
Axiom of probabilityは、g-formulaに応用することもできます。
疫学研究における因果推論を語るなら、必須の考え方ですね。
実際に以下のDAGでg-formulaを定義してみましょう。

- E(Yx) *Potential Outcome
- = ΣcE(Yx, C) *Law of total probability
- = ΣcE(Yx|C)P(C) *Chain rule
- = ΣcE(Yx|X, C)P(C) *Conditional independence
- = ΣcE(Y|X, C)P(C) *Consistency
となります。これがg-formulaです。
これまでのaxiomとconsistency(後日説明します)のみで証明可能です。
Bias Analysesについて
最後にBias analysesへの応用について説明しましょう。まず以下のDAGを見てください。
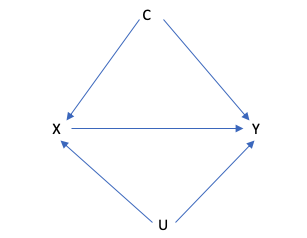
このDAGで、X, C, Yしか計測できず、Uは計測不可能でした。
この場合、Y, X, Cの変数を使って因果推論をしようにも、バイアスを排除することができません。
この時もaxiom of probabilityを使用して、bias analysisに持ち込みます。
例として、以下のようにできます。例えばYにXとCでregressionをして、P(Y|X, C)を計測したとして、以下のように発展させることができます。
- P(Y|X, C)
- = ΣuP(Y|X, C, U)P(U|X, C)
例えば、
- P(Y|X, C) = φ0 + φxX + φcC
とします。しかし、本当に欲しかった統計モデルはこちらです。
- P(Y|X, C, U) = β0 + βxX + βcC+ βuU
さらに、P(U|X, C)が、
- P(U|X, C) = γ0 + γxX + γcC
と想定します。P(Y|X, C) = ΣuP(Y|X, C, U)P(U|X, C)の数式を解くと、
- ΣuP(Y|X, C, U)P(U|X, C)
- = β0 + βxX + βcC+ βu(γ0 + γxX + γcC)
- = (β0 +βuγ0)+ (βx+ βuγx)X + (βc+βuγc)C
- = φ0 + φxX + φcC
となります。私たちが欲しい値はφxではなく、βxですので、以下の等式で解決します。
- βx = φx – βuγx
これをbias formulaと言います。また、「βuγx」のことをbias factorと呼びます。
逆説的にいうと、「βuγx」を過去の研究から得ることができれば、バイアス解析が可能になると言えます。
まとめ
今回は疫学研究のおける確率を知る上で重要な6つの公理について解説してきました。
本来、疫学のトレーニングを受ける場合、
- DAGからData generation processを考える
- 具体的に確率での表記をする
- Axiom of probabilityからみて正しいかを確認する
- 疫学手法の背景を確率から理解する
といった基本的な理解が必要なのですが、随分と軽視されている印象もあります。
今回の解説が、疫学研究を行う人、疫学のトレーニングを受けている人の確率の理解の一助になればと思います。