P値とは「偶然だけでそのデータを観測する確率」ではなく、正しくは「(研究にバイアスがなく使用した統計モデルに誤りがない条件で)帰無仮説が真のときに、統計的要約が実際の観測結果以上になる確率」と前回説明してきました。
P値は確率ですので0〜1の間におさまります。しかし、0.05というカットオフ値をつけてしまうと、P < 0.05であれば統計学的に有意、P > 0.05であれば有意でないと分けてしまいます。この弊害として、たった0.002の違いですが、P = 0.049であれば有意になり、P = 0.051では有意でなくなります。しかし、この0.002の差にほとんど意味がありませんが、前者は治療効果がある/因果関係があると過剰に報告され、後者は本当は治療効果がある可能性も残しているのに「関連性なし」とばっさりと切り捨てられてしまいます。
このようにP = 0.05を基準にして「あり/なし」と過度に二分しすぎる人のことを「ダイコトマニア(dichotomania)」と表現する疫学者もいます。
なぜこの現象が起こったのか、1つはP値が0〜1という狭い範囲で計測しているため、研究者の認知に誤解が生じやすい特徴があります、この特徴を改善させる方法にS-valueという考え方があります。
CompatibilityでP値を考える
まずはcompatibilityという考え方でP値を考えてみましょう。研究にバイアスがなく使用した統計モデルに誤りがない条件下での話である点にも注意してください。
Compatibilityとは、適合性などと日本語訳をつけることができますが、疫学研究でアウトカムを比較する場合、計測されたデータ(平均の差やリスク比、オッズ比など)が帰無仮説とどれだけ適合しているか(compatible)をP値という指標で計測していると考えてみましょう。
例えば、P値が1.00であれば、平均差であれば0に、リスク比やオッズ比であれば1になります。つまり、これは計測された結果が帰無仮説に完全に適合しているといえます(Perfect compatibility)。
逆に、P値が1から離れて0に近くにつれて、帰無仮説と計測された結果の適合性は崩れます。このことをincompatibilityといいます。P = 1.00がperfect compatibilityであれば、P = 0.00はperfect incompatibilityといえます。

しかし、この帰無仮説と計測されたデータでのcompatibility/incompatibilityの考え方も不十分です。たとえば、
- P = 0.005 vs.P = 0.05
- P = 0.95 vs. P = 0.995
を比較した場合、P値を計算する上で、前者(P = 0.005 vs. P = 0.05)の違いは大きいでが、後者(P = 0.95 vs. P = 0.995)は小さいです。
といっても理解が難しいと思うので、実際のZ-scoreやχ-scoreとP値を比較してみましょう。
|
P値 |
0.005 |
0.05 |
0.95 |
0.995 |
|
Z-score |
3.48 |
1.96 |
0.06 |
0.006 |
|
χ3 |
4.21 |
2.80 |
0.59 |
0.12 |
|
χ9 |
5.45 |
4.11 |
1.82 |
0.99 |
例えばz-scoreでみてみると、P = 0.995とP = 0.95は0.045の差ですがZ-scoreでは0.054です。一方で、P = 0.005とP = 0.05は、P値での差は同じ0.045ですが、Z-score上では1.52もの違いがあります。
|
|
Pの差 |
Zの差 |
|
P = .995 vs. P=.95 |
0.045 |
0.054 |
|
P = .005 vs. P=.05 |
0.045 |
1.52 |
P値をcompatible/incompatibleというだけでは、実際にどのくらいZ-scoreやχ-scoreの変化が大きいのかという点を捉えきれません。
S-valueとは?
ここから先も、くどいようですが、研究にバイアスがなく、使用した統計モデルに誤りがない条件下での話である点にも注意してください。
私たちが知りたいのは、計測したデータが帰無仮説からどれくらいかけ離れているのか、どのくらい極端なのかという点です。これを捉えるのにP-valueという確率では不十分であり、場合によってはミスリードしてしまう点を説明してきました。
研究にバイアスがなく、使用した統計モデルに誤りがない条件下で「計測したデータが帰無仮説からどれくらいかけ離れているか」という距離を別の指標としてS-valueがあり7、P-valueの欠点を補うことができます3。
S-valueはP-valueをlogで変換することで計測可能で、具体的には以下のような数式になります:
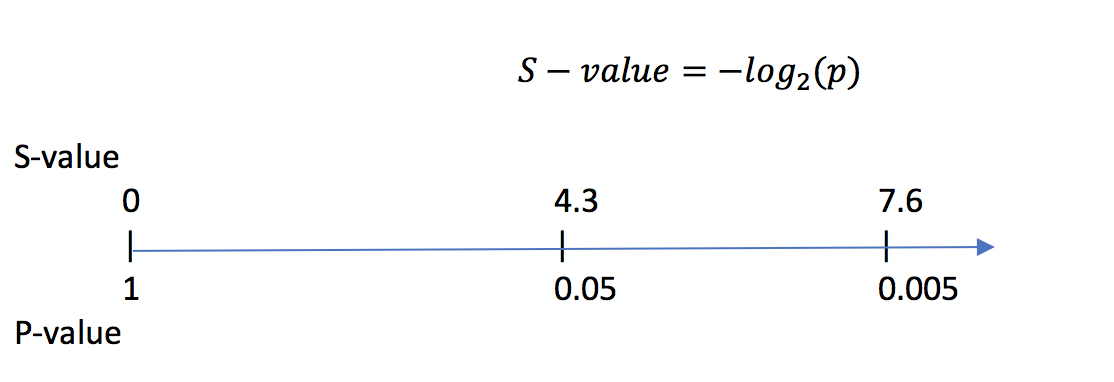
S-valueの分かりやすい点ですが、Pが小さくなればなるほど、つまり計測されたデータが帰無仮説から離れるほど、S値が上昇する点です。つまり、計測データと帰無仮説の距離を直感的に理解できる点です。
さらにlog2( )をつかっているため、P値をコイントスで考えることもできます。例えばP = 0.05はS = 4.3でしたが、これはコイントスをして表が4回ほど連続して出現するくらいの確率です(4.3に最も近い整数は4)。P = 0.005はS = 7.6でしたが、これはコイントスをして表が8回ほど連続して出現する確率です(7.6に最も近い整数は8)。
こう考えると、コイントスをして4回連続で表になるのは割とありえそうですが、8回連続というとかなり起こりづらい現象と直感的に理解できると思います。
S-valueについて気をつけておきたいこと
S-valueの説明をしてきましたが、「じゃあP-valueはやめて、S-valueにすべきなの?」と疑問に思う方もいたかもしれません。
ですが、P-valueを報告すべき、S-valueを報告すべきなどと「P-value vs. S-value」で対立させて考えるべきではありません。そもそもS-valueはP-valueを対数化しただけで、P-valueで起こりがちな認知の歪みを補正してくれるだけです。つまり、P-valueでは捉えづらかった「計測されたデータと帰無仮説の距離」を数式的に捉えやすいという利点がS-valueにはあるというだけです。
P-valueは「(研究にバイアスがなく使用した統計モデルに誤りがない条件で)帰無仮説が真のときに、統計的要約が実際の観測結果以上になる確率」として意義があります。この理解に役立つのがS-valueというだけでして、P-valueをやめるべきという考えにはならない点に注意してください。
参考文献
- Rothman, K., Greenland, S. & Lash, T. Modern Epidemiology, 3rd Edition. (Lippincott Williams & Wilkins., 2012). doi:8184731124
- Holman, C. D. A. J., Arnold-Reed, D. E., De Klerk, N., McComb, C. & English, D. R. A psychometric experiment in causal inference to estimate evidential weights used by epidemiologists. Epidemiology12, 246–255 (2001).
- Greenland, S. Valid P-Values Behave Exactly as They Should: Some Misleading Criticisms of P-Values and Their Resolution With S-Values. Am. Stat.73, 106–114 (2019).
- Brown, H. K. et al.Association between serotonergic antidepressant use during pregnancy and autism spectrum disorder in children. JAMA – J. Am. Med. Assoc.317, 1544–1552 (2017).
- Brown, H. K., Hussain-Shamsy, N., Lunsky, Y., Dennis, C. L. E. & Vigod, S. N. The association between antenatal exposure to selective serotonin reuptake inhibitors and autism: A systematic review and meta-analysis. J. Clin. Psychiatry78, e48–e58 (2017).
- Amrhein, V., Greenland, S. & McShane, B. Scientists rise up against statistical significance. Nature567, 305–307 (2019).
- Shannon, C. E. A Mathematical Theory of Communication. Bell Syst. Tech. J.27, 379–423 (1948).
- VanderWeele, T. J. & Ding, P. Sensitivity Analysis in Observational Research: Introducing the E-Value. Ann. Intern. Med.167, 268 (2017).
- Victora, C. G. et al.Evidence for protection by breast-feeding against infant deaths from infectious diseases in Brazil. Lancet (London, England)2, 319–22 (1987).